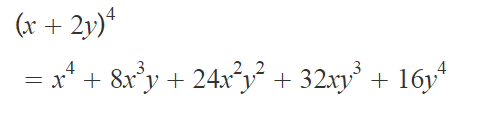
You were close, but lets see what went wrong:
First let me rearrange the terms of your expression in descending #x# exponents:
#(x+color(blue)(2y))^4 ?=? x^4+8x^3color(red)(y)+12x^2color(red)(y)^2+8xcolor(red)(y)^3+2color(green)(y)^4#
which I assume you got from
#(x+color(red)(2y))^4 ?=? x^4+4x^3*color(green)(2)color(red)(y)+6x^2*color(green)(2)color(red)(y^2)+4x^1*color(green)(2)color(red)(y^3)+color(green)(2)color(red)(y^4)#
It is not just the #color(red)(y)# that needs to be raised to various exponents but #(color(blue)(2y))#
#(x+color(blue)(2y))^4=x^4(color(blue)(2y))^0+4x^3(color(blue)(2y))^1+6x^2(color(blue)(2y))^2+4x(color(blue)(2y))^3+(color(blue)(2y))^4#
#(x+color(blue)(2y))^4=x^4(color(blue)(1))+4x^3(color(blue)(2y))+6x^2(color(blue)(4y^2))+4x(color(blue)(8y^3))+(color(blue)(16y^4))#
#(x+2y)^4 = x^4+8x^3y+24x^2y^2+32xy^3+16y^4#

