Question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region `y = 1 + x^2`, `y = 0`, `x = 0`, `x = 2` rotated about the x-axis?

Answer 1

See explanation below.

Explanation:

Here is the region to be revolved about the `x` axis:

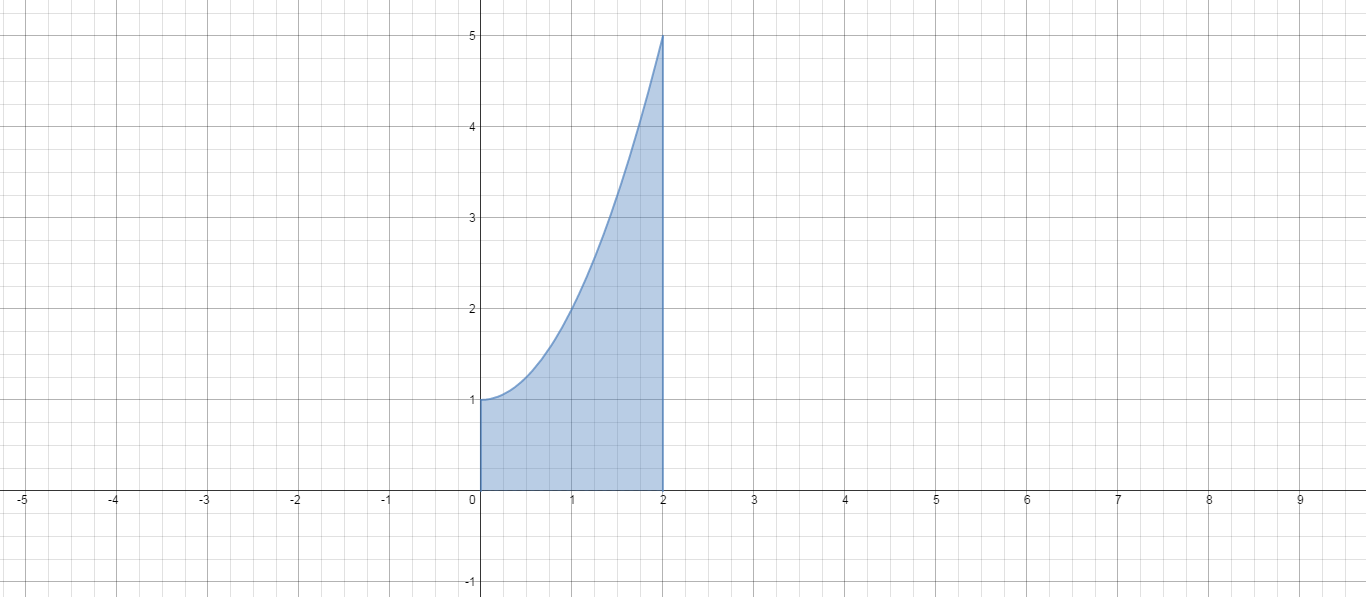
If we must use shells, we will need to take our representative slices horizontally and use thickness `dy`.

We need to rewrite the boundaries as functions of `y` so the curve becomes `x=sqrt(y-1)`.
Note that, in the region `y` varies from `0` to `5`. The radius of the shells will involve `y` values.
For the 'height' of the shell (which is lying on its side), we will use the `x` on the right minus the `x` on the left.

For `y = 0` to `1`, the 'height' is `2-0=2`, The resulting solid is a cylinder with radius `1` and height `2`. Its volume is `2pi`.
(We could do an integral for this, but we learned the volume of a cylinder in geometry class.)

From `y=1` to `y=5`, the 'height' is `2-sqrt(y-1)`.
The radius of the representative shell is `y` and the thickness is `dy`

We integrate:

`int 2 pi rh dy = 2 pi int_1^5 y(2-sqrt(y-1))dy = (176pi)/15`

Adding the two volumes, we get:

`V = 2pi+176/15 pi = 206/15 pi`

Note
If we had been allowed to use disks, we would integrate:

`pi int_0^2 (1+x^2)^2 dx = pi int_0^2 (1+2x^2+x^4) dx`

`= pi [x+(2x^3)/3 + x^5/5]_0^2`

`= pi [2+16/3+32/5] = pi [(30+80+96)/15] = 206/15 pi`

Of course, we get the same answer, but we only need to do one calculation and the integral is (I think) simpler.