Question

Is it possible to distinguish between first and second-order reactions based on a `[A]` vs. time graph?

Answer 1

If you are finding `(d[A])/(dt)` at each moment in time, that means you are finding the slope at each point on a graph of the change in concentration versus time.

The graphs would look like:

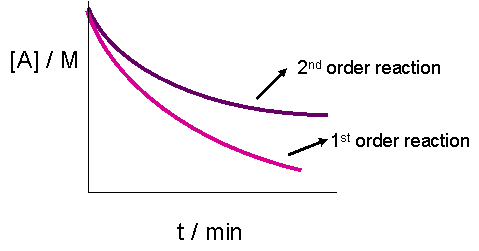
Without looking at both cases, it is impossible to tell by a graph. Even when superimposing both on the same graph, it may be hard to tell if it's really a second order vs. first order, or if it's just because a different mechanism occurred by accident that happened to give you that exact graph.

A zero order reaction is linear, though, so that you can distinguish from a first or second order reaction.

---

A better way to tell is by looking at a table. Let's suppose we have this (made-up) data:

`N_2 + O_2 -> 2NO`

`" "" "" "" "[N_2] (M)" "[O_2] (M)"" " "r(t)(s^(-1))`
Trial 1: `" "" "\mathbf(0.1)" "" "" "\mathbf(0.2)" "" "" " 1xx10^(-5)`
Trial 2: `" "" "0.1" "" "" "\mathbf(0.4)" "" "" " 4xx10^(-5)`
Trial 3: `" "" "\mathbf(0.2)" "" "" "0.2" "" "" " 2xx10^(-5)`

If you look at the trial concentrations I bolded, note the change in concentration of `N_2` and `O_2`.

`N_2`:
- doubled concentration
- rate of reaction doubled

`[([N_2]_f)/([N_2]_i)]^x = (r(t)_f)/(r(t)_i)`

`[2]^x = 2`
`x = 1`

Thus, the reaction is first order in `N_2`.

`O_2`:
- doubled concentration
- rate of reaction quadrupled

`[([O_2]_f)/([O_2]_i)]^x = (r(t)_f)/(r(t)_i)`

`[2]^x = 4`
`x = 2`

Thus, the reaction is second order in `O_2`.

For this reaction then, you can write:

`color(blue)(r(t) = k[N_2][O_2]^2)`