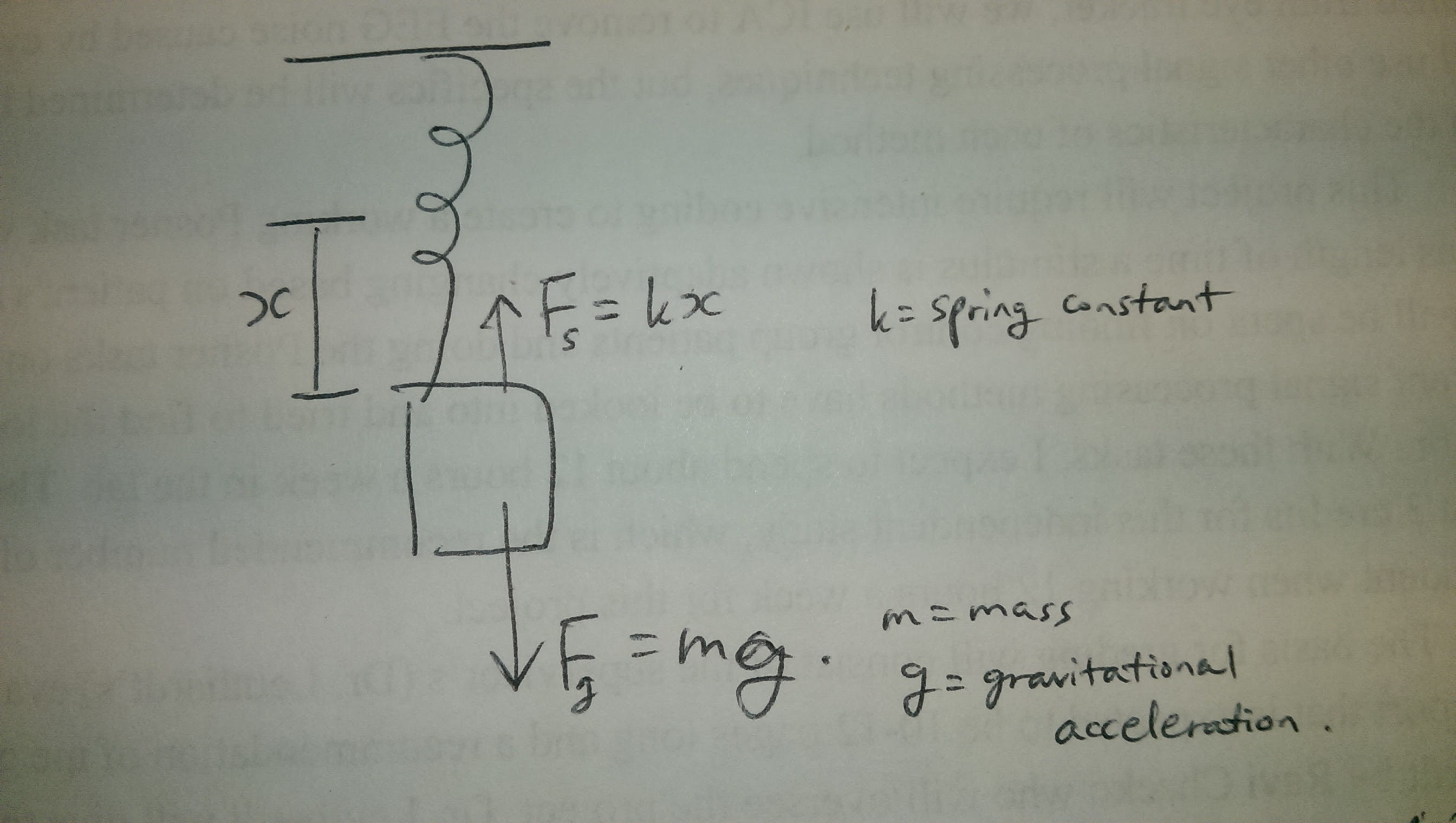
At any time, the net force is gravitational force - spring force.
Thus, I write this equation: m(d^2x)/dt^2+10x=mg
10 is the spring constant k.
The equation for this system is
x(t)=c_4cos(sqrt(10/m)t)+c_5sin(sqrt(10/m)t)+mg.
(If you want to know more about how this is derived. Look below to Heavy Math Part section.)
c_4 and c_5 cannot be determined without more information, such as value of x(0) when t=0.
However, we can still use this equation to find the oscillation frequency. The only oscillatory components are c_4cos(sqrt(10/m)t) and c_5sin(sqrt(10/m)t).
For frequency to be 1, sqrt(10/m)=2pi which means m=0.253.
Since frequency is not dependent on g, the mass to create frequency of 1s^-1 or period of 1s would be 0.253 kg on both Earth and Mars.
Heavy Math Part
So what we have now is a second-order nonhomogeneous differential equation.
We first solve the left-hand side. That is: m(d^2x)/dt^2+10x=0
Substituting dx/dt with s gives ms^2+10=0.
Solving for s gives s=sqrt(10/m)i, -sqrt(10/m)i.
The general solution becomes x(t)=c_1e^(sqrt(10/m)i)+c_2e^(-sqrt(10/m)i)+c_3.
Substituting Euler's formula e^(it)=cos(t)+isin(t) gives x(t)=c_1(cos(sqrt(10/m)t)+isin(sqrt(10/m)t))+c_2(cos(sqrt(10/m)t)-isin(sqrt(10/m)t))+c_3.
To get rid of imaginary components, we assume c_1 and c_2 to be multiples of certain c_1 and c_2 values.
If c_1=c_2=c_4/2, x(t)=c_4cos(sqrt(10/m)t).
If c_1=c_5/(2i) and c_2=-c_5/(2i), x(t)=c_5sin(sqrt(10/m)t)
Now we have an equation without imaginary components:
x(t)=c_4cos(sqrt(10/m)t)+c_5sin(sqrt(10/m)t)+c_3.
We are done with the left side of the first equation. Now we find c_3 using right side of the first equation.
(d^2x)/dt^2=-10c_4/mcos(sqrt(10/m)t)-10c_5/msin(sqrt(10/m)t)
m(d^2x)/dt^2+10x=-10c_4cos(sqrt(10/m)t)-10c_5sin(sqrt(10/m)t)+10c_4cos(sqrt(10/m)t)+10c_5sin(sqrt(10/m)t)+c_3=c_3=mg
Thus, x(t)=c_4cos(sqrt(10/m)t)+c_5sin(sqrt(10/m)t)+mg.

