Question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region `y=2x^2+5`, `y=x+3`, the y-axis, and the line `x=3` rotated about the x-axis?

Answer 1

See the explanation section, below.

Explanation:

Here is a graph of part of the region to be rotated about the `x` axis.

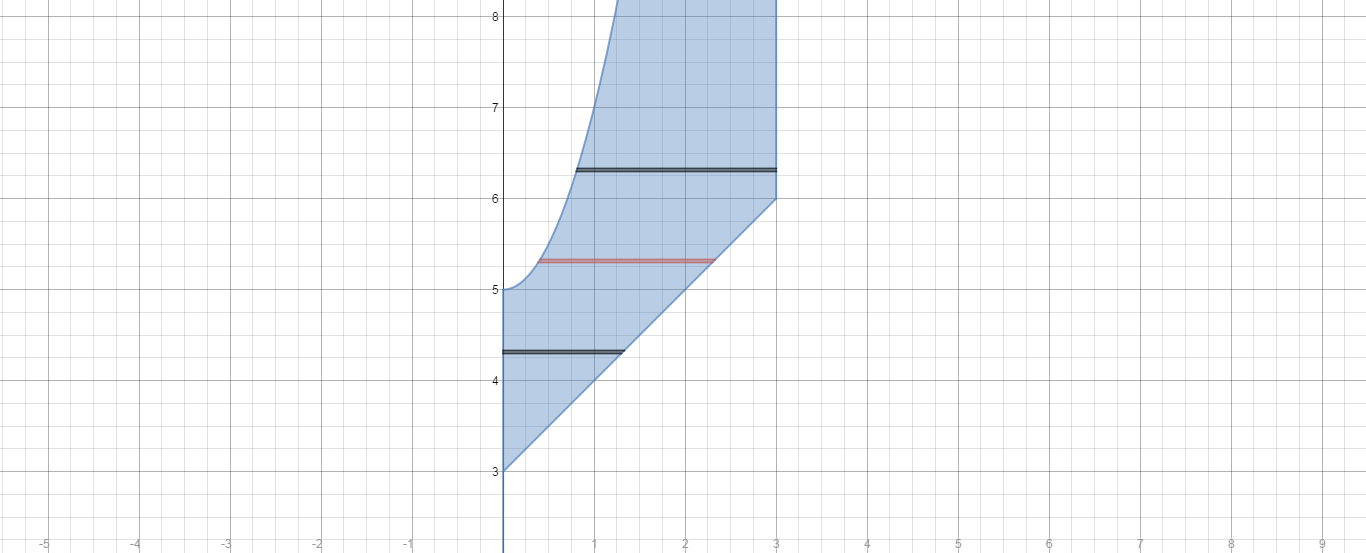
In order to use shells, we must take our representative slice parallel to the axis of rotation. In this case, that's the `x` axis, so the thickness of our shells will be `dy`.

That means we'll need to rewrite the curves as functions of `y`

`x=sqrt((y-5)/2)`, `x=y-3`

Every shell will have `"radius" =y`, `"thickness"=dy` and `"height" = x_"right" - x_"left"`

As the graph shows, there are three separate integrals we need to do, because the calculation of `x_"right"` and `x_"left"` change as `y` goes from `3` (the lower bound) to `23` (the uppr bound, not on my graph).

(Are we sure we want to use shells for this?)

From `y=3` to `y=5` , the height of the cylindrical shell will be
`"height" = x_"right" - x_"left" = (y-3)-0 = y-3`

So we need to integrate

`int_3^5 2piy(y-3)dy = 2pi int_3^5 (y^2-3y)dy` which is left to the student.

From `y=5` to `y=6`, the height of the cylindrical shell will be
`"height" = x_"right" - x_"left" = (y-3)- sqrt((y-5)/2)`

So we need to integrate

`int_5^6 2piy(y-3- sqrt((y-5)/2))dy = 2pi int_5^6 (y^2-3y- ysqrt((y-5)/2))dy` the last term of which can be integrated by substitution (or parts).

From `y=6` to `y=23`, the height of the cylindrical shell will be
`"height" = x_"right" - x_"left" = 3- sqrt((y-5)/2)`

So we need to integrate

`int_6^23 2piy(3- sqrt((y-5)/2))dy = 2pi int_6^23 (3y- ysqrt((y-5)/2))dy` the last term of which can be integrated by substitution (or parts).

Washers

To use washers take the slices perpendicular to the axis of rotation.

As x varies from `0` to `3`, the greater radius at `x` is `R = 2x^2+5` and the lesser radius is `r = x+3`,

We need to integrate

`int_0^3 pi (R^2-r^2)dx = pi int_0^3 ((2x^2+5)^2-(x+3)^2)dx` which is simply the integral of a degree 4 polynomial when we expand it.