What is the perimeter of a rhombus with diagonals 10 and 24?

Question

9910 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-11-15T05:46:58

The Pythagoras' theorem comes in handy here.

enter image source here

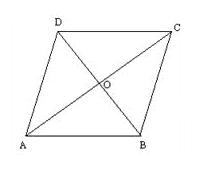
useruploads.socratic.org

ABCD is our rhombus with the diagonals #AC = 24# units and #BD = 10# units respectively.

Now, since a rhombus is also a parallelogram, the diagonals bisect each other at the point where they meet, which in this case is O.

Therefore, #OC=OA=(AC)/2=24/2=12# units and #OB=OD=(BD)/2=10/2=5# units.

Now, in a rhombus the diagonals intersect each other at 90 degrees.

Hence, #angleBOC = 90 ^o#
In right angled triangle BOC, applying the Pythagoras' theorem, we have:

#BC=sqrt(OB^2+OC^2)#
#=> BC = sqrt(5^2+12^2)#
#=>BC = sqrt(169)#
#=>BC=13# units

Now, in a rhombus, the length of all sides are equal
i.e. #AB=BC=CD=DA#

Thus perimeter = #4*(BC)# = #4*13# = #52# units