How do you find the remainder when f(x)=x^4+8x^3+12x^2; x+1?
2 Answers
Dec 31, 2015
5
Explanation:
Simply perform long division. That is;
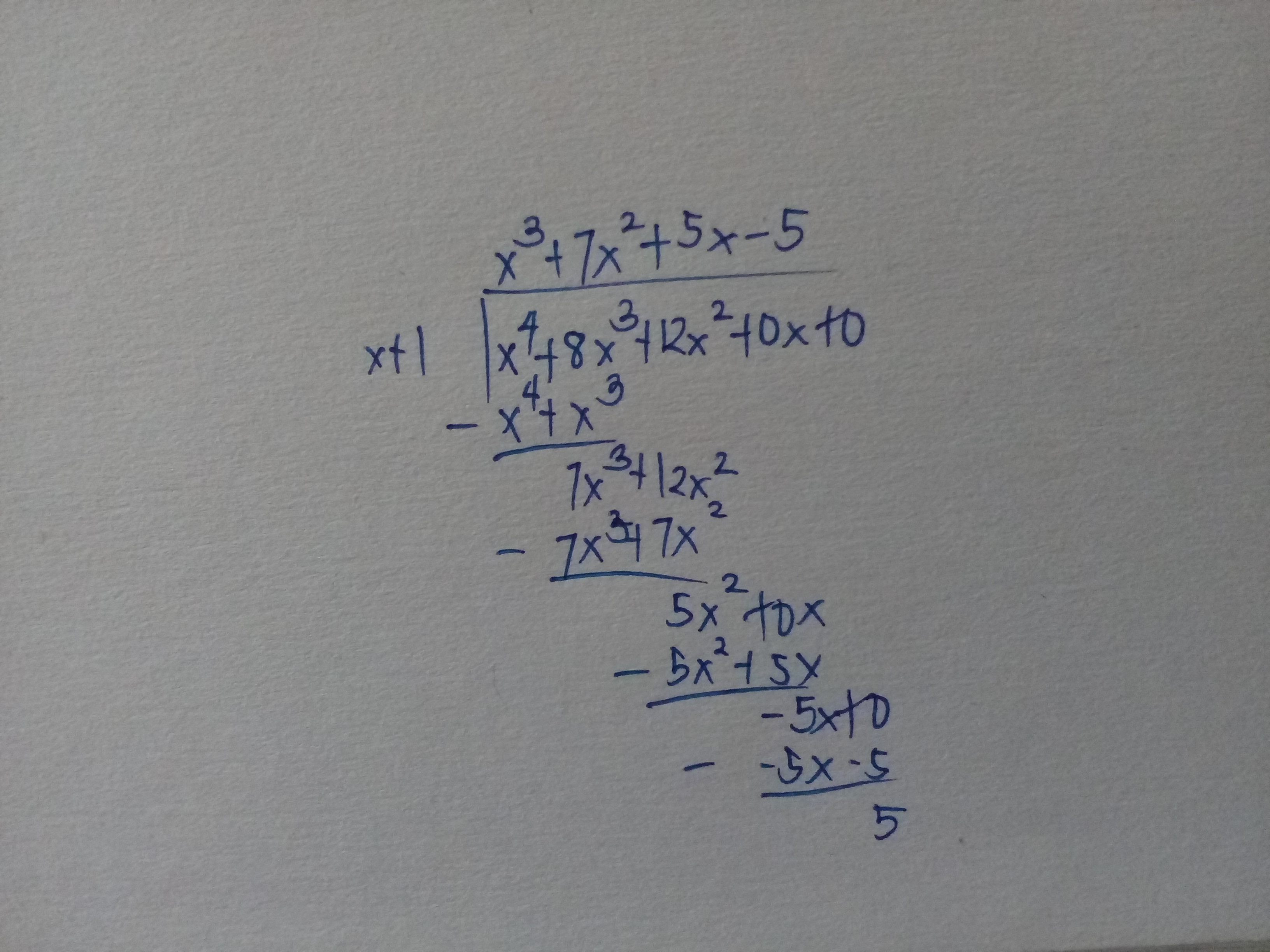
Dec 31, 2015
The remainder is
Explanation:
The remainder of dividing
In our case
f(-1) = (-1)^4+8(-1)^3+12(-1)^2 = 1-8+12 = 5

