How do you integrate #int (4^(7x)) / (5^(2x)) # using integration by parts?
3 Answers
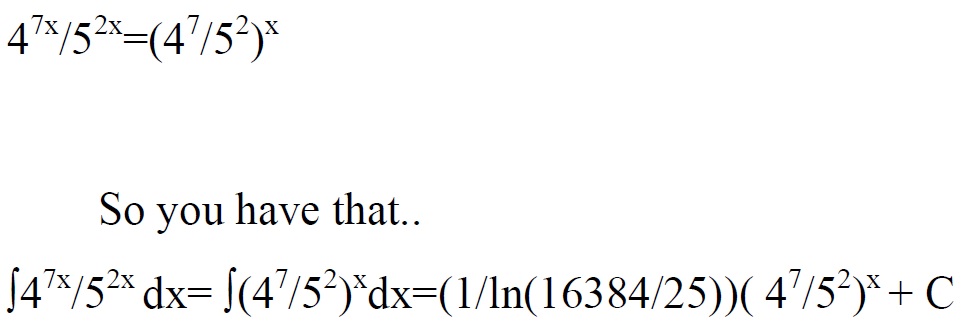
Explanation:
Hi!
I attached a quick jpg image of what you should do.
I'll get more familiar with Socratic's proprietary math editor, but hopefully this will suffice for now. Just use properties of exponents and integrate. You can use parts, but I believe that is much more involved and sort of counterproductive.
Let me know if this makes sense!
Ken
where
Explanation:
where
Explanation:
Since you did ask for integration by parts
Or, rewriting it a little
Saying
And
The latter integral is the same as



