Refer to figure below. (Obs.: D is the circle's center)
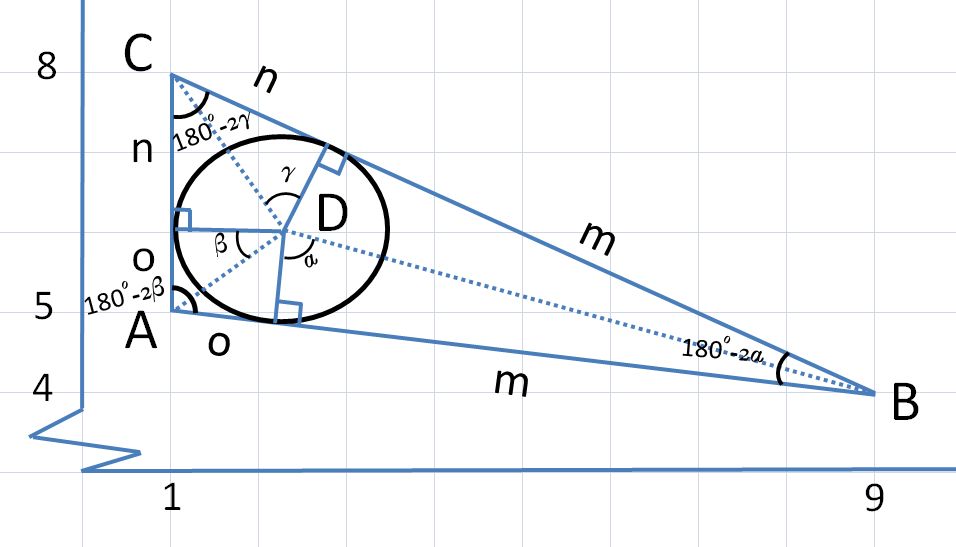
With #A(1,5), B(9,4) and C(1,8)#
#AB=sqrt((9-1)^2+(4-5)^2)=sqrt(64+1)=sqrt(65)~=8.1#
#BC=sqrt((1-9)^2+(8-4)^2)=sqrt(64+16)=sqrt(80)=4sqrt(5)~=8.9#
#CA=sqrt((1-1)^2+(5-8)^2)=3#
Using the variables #m, n and o#
#m+n=4sqrt(5)#
#m+o=sqrt(65)#
#n+o=3# => #o=3-n#
=> #m+3-n=sqrt(65)# => #m-n=sqrt(65)-3#
Adding the last with the first equation, we get
#2m=4sqrt(5)+sqrt(65)-3# => #m=2sqrt(5)+sqrt(65)/2-1.5#
In the figure we can see that
#tan alpha=r/m# => #r=m*tan alpha#
We only need to know #alpha#
Using vectors
#BvecA=(1-9)hat i+(5-4)hat j=-8hat i+hat j#
#BvecC=(1-9)hat i+(8-4)hat j=-8hat i+4hat j#
#cos (2alpha)=(BvecA*BvecC)/(|BA|*|BC|)=(8*8+1*4)/(sqrt(65)*4sqrt(5))=68/(20sqrt(13))=17/(5sqrt(13))#
=> #2alpha=19.440^@# => #alpha=9.720^@#
Using the Law of Sines
#3/sin(180^@-2alpha)=sqrt(65)/sin(180^@-2beta)=(4sqrt(5))/sin(180^@-2gamma)#
Since sines of supplementary angles are equal we can rewrite the previous equation as
#3/(sin 2alpha)=sqrt(65)/(sin 2beta)=(4sqrt(5))/(sin 2gamma)#
#3/(sin 2alpha)=sqrt(65)/(sin 2beta)# => #sin 2beta=sqrt(65)/3*sin 2alpha#
We know also that #2alpha+2beta+2gamma=180^@# => #2gamma=180^@-2alpha-2beta#
So
#3/sin(2alpha)=(4sqrt(5))/sin(180^@-2alpha-2beta)=(4sqrt(5))/sin (2alpha+2beta)=(4sqrt(5))/(sin 2alpha *cos 2beta+sin 2beta *cos 2alpha)#
#-> 3/cancel (sin2alpha)=##(4sqrt(5))/(cancel(sin 2alpha)*sqrt(1-65/9*sin^2 2alpha)+sqrt(65)/3*cancel(sin 2alpha) *sqrt(1-sin^2 2alpha)#
#-> cancel(3)*sqrt(9-65sin^2 2alpha)/cancel(3)+cancel(3)*sqrt(65)/cancel(3)*sqrt(1-sin^2 2alpha)=4sqrt(5)#
#-> (sqrt(9-65sin^2 2alpha))^2=(4sqrt(5)-sqrt(65)*sqrt(1-sin^2 2alpha))^2#
#-> 9-cancel(65sin^2 2alpha)=80-8*5*sqrt(13)*sqrt(1-sin^2 2alpha)+65-cancel(65sin^2 2alpha)#
#40sqrt(13)*sqrt(1-sin^2 2alpha)=136#
#1300-1300*sin^2 2alpha=1156# => #sin^2 2alpha=144/1300# => #sin 2alpha=6/(5sqrt(13))# => #2alpha=19.440^@# => #alpha=9.720^@#
Finally,
#r=m*tan alpha=(2sqrt(5)+sqrt(65)/2-1.5)*tan 9.720^@# => #r=1.220#


