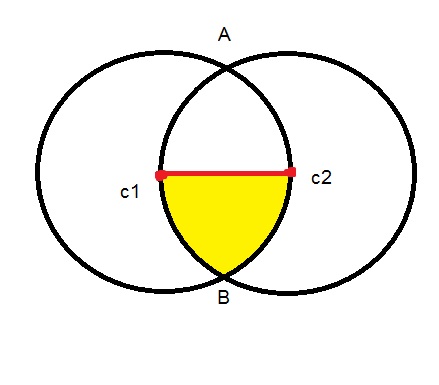
the points c1 and c2 are centers of the two equal circles shown in the figure. if the distance between the center is 3 cm, find the area of the shaded region?
1 Answer
Explanation:
First let's call "
Since
If we consider the
Since the area of the circle1 is
The area defined by the arc
#S_(triangle_(BC_1D))=(b*h)/2=(BD*C_1D)/2=((rsqrt(3))/2*r/2)/2=r^2sqrt(3)/8#
Then
#S_(BC_2D)=(pi*r^2)/6-r^2sqrt(3)/8=r^2/24(4pi-3sqrt(3))#
Since the two circles are equal

