Question #15b5e

1 Answer
Rui D.
Feb 2, 2016

The circle with the equation #(x-3/2)^2+(y+7/4)^2=(9/8)^2# or #64x^2+64y^2-192x+224y+259=0#

Explanation:

Since the distance from the center of the original circle to any midpoint in a chord spanning a constant central angle is also constant , the locus asked for is other circle with a shorter radius but the same center of the larger circle, as we can see in Fig. 1
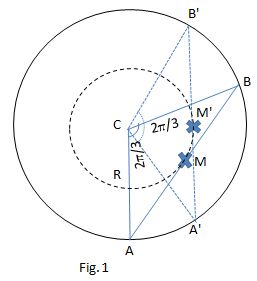
I created this figure using MS Excel

The equation of the larger circle is
#4x^2+4y^2-12x+14y+1=0#
#x^2+y^2-3x+7/2y+1/4=0#

#-2x_0=-3# => #x_0=3/2#
#-2y_0=7/2# => #y_0=-7/4#
#x_0^2+y_0^2-R^2=1/4# => #R^2=9/4+49/16-1/4# => #R=sqrt(36+49-4)/4=sqrt(81)/4# => #R=9/4#
#-> (x-3/2)^2+(y+7/4)^2=(9/4)^2#

To find the shorter radius (#r#) consider the #triangle_(ABC)# whose sides are the chord #AB# and two radii #R# as shown below
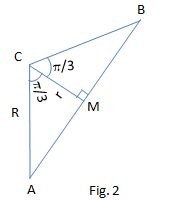
I created this figure using MS Excel

Since the segment CM acts as a bisector of chord AB and therefore #A hat C M=(1/2) A hat C B=pi/3#, we can see that
#cos (pi/3)=r/R# => #r=Rcos (pi/3)=9/4*1/2# => #r=9/8#

So the equation of the shorter circle is

#->(x-3/2)^2+(y+7/4)^2=(9/8)^2#
Or
#x^2-3x+9/4+y^2+7/2y+49/16-81/64=0#
#x^2+y^2-3x+7/2y+(144+196-81)/64=0#
#x^2+y^2-3x+7/2y+259/64=0#
#->64x^2+64y^2-192x+224y+259=0#

Related questions
Impact of this question
1242 views around the world
You can reuse this answer
Creative Commons License