Question

A superhero launches himself from the top of a building with a velocity of 7.3m/s at an angle of 25 above the horizontal. If the building is 17 m high, how far will he travel horizontally before reaching the ground? What is his final velocity?

Answer 1

A diagram of this would look like this:

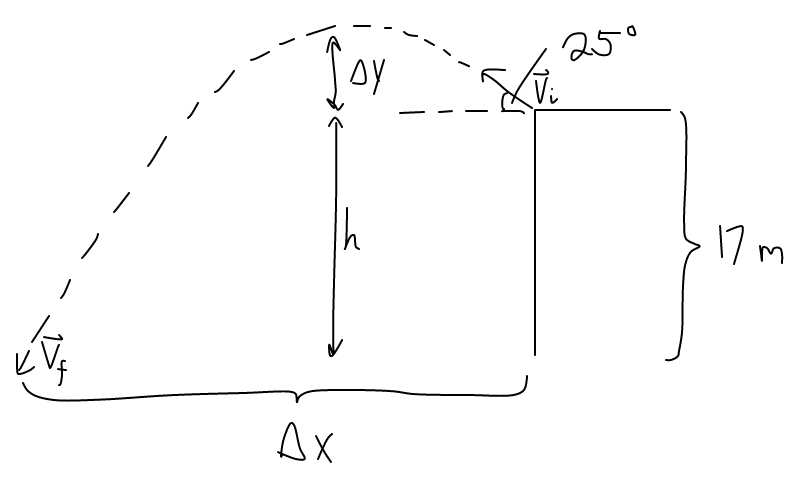
What I would do is list what I know. We will take negative as down and left as positive.

`h = "17 m"`
`vecv_i = "7.3 m/s"`
`veca_x = 0`
`vecg = -"9.8 m/s"^2`

`Deltavecy = ?`
`Deltavecx = ?`
`vecv_f = ?`

PART ONE: THE ASCENSION

What I would do is find where the apex is to determine `Deltavecy`, and then work in a free fall scenario. Note that at the apex, `vecv_f = 0` because the person changes direction by virtue of the predominance of gravity in decreasing the vertical component of the velocity through zero and into the negatives.

One equation involving `vecv_i`, `vecv_f`, and `vecg` is:

`\mathbf(vecv_(fy)^2 = vecv_(iy)^2 + 2vecgDeltavecy)`

where we say `vecv_(fy) = 0` at the apex.

Since `vecv_(fy)^2 < vecv_(iy)^2` and `Deltavecy > 0`, `Deltavecv_y^2 < 0` and this equation is indeed asking us to use `g < 0`.

For part 1:

`color(blue)(Deltavecy) = (vecv_(fy)^2 - v_(iy)^2)/(2g) = color(blue)((-v_(iy)^2)/(2g)) > 0`

where `vecv_(fy) = 0` is the final velocity for part 1.

Recall that a vertical velocity has a `sintheta` component (draw a right triangle and get the `sintheta = (vecv_(y))/(vecv)` relationship).

`color(green)(Deltavecy = (-v_(i)^2 sin^2theta)/(2g)) > 0`

Now that we have `Deltavecy` and we know that `vecv_y` has changed direction, we can suppose free fall is occurring.

The total height of the fall is `color(green)(h + Deltavecy)`. That is something we can use for part 2.

I get `Deltavecy` to be about `"0.485 m"` and `h + Deltavecy` to be about `color(blue)("17.485 m")`.

PART TWO: THE FREE FALL

We can again treat the `y` direction independently of the `x` direction, since `veca_x = 0`.

At the apex, recall that `color(green)(vecv_(iy) = 0)`, which is the initial velocity for part 2, and was the final velocity in part 1. Now we can use another 2D kinematics equation. Remember that the total height is not `Deltavecy` here!

`\mathbf(h + Deltavecy = 1/2g t_"freefall"^2) + cancel(v_(iy)t_"freefall")^(0)`

Now we can just solve for the time it takes to hit the ground from the apex.

`color(green)(t_"freefall") = sqrt((2(h + Deltavecy))/g)`

`= color(green)(sqrt((2(h - (v_(i)^2 sin^2theta)/(2g)))/g))`

and of course, time is obviously not ever negative, so we can ignore the negative answer.

...And we're getting there.

PART THREE: SOLVING FOR THE HORIZONTAL DISTANCE

We can reuse the same kinematics equation as the one previously examined. One of the things we have been going for is `Deltax`, which is:

`color(blue)(Deltax) = cancel(1/2a_xt^2)^(0) + v_(ix)t`

And like before, use a trig relation to get the `x` component (`costheta`).

`= color(blue)(vecv_icostheta*t_"overall") > 0`

where `t_"overall"` is NOT what we got in part 2, but will include the time `t_"leap"` going from the building to the apex of the flight and `t_"freefall"` that we acquired earlier.

`Deltay = 1/2vecg t_"leap"^2 + vecv_(iy)t_"leap"`

With `Deltay ~~ "0.485 m"`. When we solve this using the quadratic equation, it would yield:

`t_"leap" = (-(vecv_(iy)) + sqrt((vecv_(iy))^2 - 4(1/2vecg)(-|Deltay|)))/(2*1/2vecg)`

`~~ "0.3145 s"`

Include the time acquired for apex to the ground and you should get about `color(blue)("2.20 s")` for the entire flight. Let's call this `t_"overall"`.

`t_"overall" = t_"leap" + t_"freefall"`

Using `t_"overall"`, I get `color(blue)(Deltavecx ~~ "14.58 m")`.

PART FOUR: SOLVING FOR THE FINAL VELOCITY

Now this is going to require a bit more thinking. We know that `h = "17 m"` and we have `Deltax`. Therefore, we can determine the angle with respect to the horizontal ground.

`tantheta' = (h+Deltavecy)/(Deltavecx)`

`color(blue)(theta' = arctan((h+Deltavecy)/(Deltavecx)))`

Notice how we used `h + Deltavecy` since we did in fact jump upwards before falling, and we did not jump straight forward. So, the angle `theta` involves `Deltax` and the total height, and we will take the magnitude of the total height for this.

And finally, since `vecv_x` has not changed all this time (we ignore air resistance here):

`color(green)(vecv_(fx)) = vecv_(ix) = vecv_fcostheta' = color(green)(vecv_icostheta') > 0`

where `vecv_i` is the initial velocity from part 1. Now we just need to know what `vecv_(fy)` is in part 2. Go back to the beginning to see:

`vecv_(fy)^2 = cancel(vecv_(iy)^2)^(0) + 2vecg*(h+Deltavecy)`

Hence, this becomes:

`color(green)(vecv_(fy) = -sqrt(2vecg*(h+Deltavecy))) < 0`

Remember that we defined down as negative, so `h+Deltay < 0`.

Okay, we're ALMOST there. We are asked for `vecv_f`. Therefore, we finish by using the Pythagorean Theorem.

`vecv_f^2 = vecv_(fx)^2 + vecv_(fy)^2`

`color(blue)(vecv_f = -sqrt(vecv_(fx)^2 + vecv_(fy)^2)) < 0`

Overall, `color(blue)(|vecv_f| ~~ "19.66 m/s")`.

And that would be all of it! Check your answer and tell me if it worked out.

Answer 2

Here the vel. of projection, `v=7.3ms^-1`
the angle. of projection ,`alpha=25^0` above horizontal
The upward vertical component of vel of projection ,`vsinalpha= 7.3*sin25^0 =7.3*0.42ms^-1~~3.07ms^-1`

The building being 17m high , the net vertical displacement reaching the ground will be `h=-17m` as the superhero projected himself upward (taken positive here)

If the time of flight i.e.time for reaching ground is taken to be T
then using the formula `h = vsinalpha*t-1/2*g*t^2` we can have
`=>-17=3.07*T-0.5*9.8*T^2`
`=>4.9T^2-3.07T-17=0`

dividing both sides by 4.9 we get

`=>T^2-0.63T-3.47=0`
`=>T=(0.63+sqrt((-0.63)^2-4*1*(-3.47)))/2~~2.20s`
(negative time discarded)

So Hero's Horizontal displacement before reaching ground will be
`=T*vcosalpha=2.20**7.3cos(25^0)~~14.56m`

Calculation of velocity at the time of reaching ground

Vertical component velocity at the time of reaching ground

`v_y^2= u^2sin^2alpha+2xx(-9.8)xx(-17)`

Again horizontal component of the velocity at the time of reaching ground

`=>v_x=ucosalpha`

So resultant velocity at the time of reaching ground

`v_r=sqrt(v_x^2+v_y^2)=sqrt(u^2sin^2alpha+u^2cos^2alpha-2xx9.8xx17)`

`=>v_r=sqrt(u^2+2xx9.8xx17)`

`=>v_r=sqrt(7.3^2+2xx9.8xx17)=19.66"m/s"`

Direction of `v_r` with the horizontal`=tan^-1(v_y/v_x)`

`=tan^-1(sqrt(u^2sin^2alpha+2xx(-9.8)xx(-17))/(ucosalpha))`

`=tan^-1(sqrt(7.3^2sin^2 25+2xx(-9.8)xx(-17))/(7.3cos25))`
`=70.3^@->"downward with the horizontal"`

Is it helpful ?