A circular curve of highway is designed for traffic moving at 92 km/h. When assumed the traffic consists of cars without negative lift ?
(a) If the radius of the curve is 150 m, what is the correct angle of banking of the road? (b) If the curve were not banked, what would be the minimum coefficient of friction between tires and road that would keep traffic from skidding out of the turn when traveling at 92 km/h?
(a) If the radius of the curve is 150 m, what is the correct angle of banking of the road? (b) If the curve were not banked, what would be the minimum coefficient of friction between tires and road that would keep traffic from skidding out of the turn when traveling at 92 km/h?
1 Answer
(a)
(b)
Explanation:
 http://hyperphysics.phy-astr.gsu.edu/hbase
http://hyperphysics.phy-astr.gsu.edu/hbase
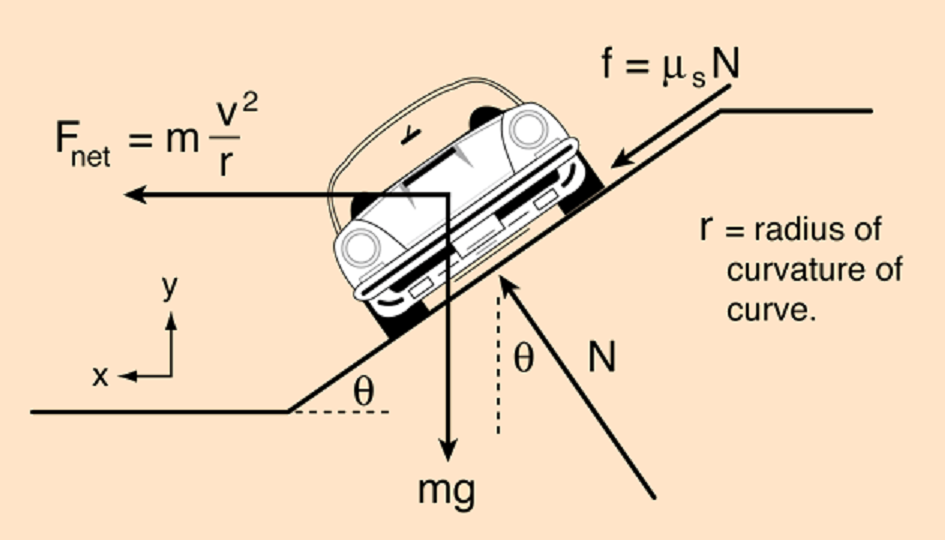
(a) In the figure above
Let
We know that while in circular motion the centripetal force acting on the car
And force due to friction is given as
Assuming car to be situated at the origin, Force equations in the
For designing of banking angle of the curved roads, worst case is considered.
Very low values of
Above equations reduce to
Dividing first with second we obtain
or
Given
Inserting all values in above expression
(b) If curves are not banked, implies that
Insert value of
We observe that this is equal to value of
