(A)
Carbonic acid is a weak diprotic acid with 2 ionisations:
#H_2CO_3rightleftharpoonsHCO_3^(-)+H^+" "K_(a1)=4.27xx10^(-7)"mol/l"#
#HCO_3^(-)rightleftharpoonsCO_3^(2-)+H^(+)" "K_(a2)=4.68xx10^(-11)"mol/l"#
In the flask we have #20.00"ml"# of #0.10"M"# sodium carbonate. As the acid is run in from the burette the following reaction occurs as the carbonate ion becomes protonated:
#CO_3^(2-)+H^+rarrHCO_3^(-)#
The initial number of moles of #CO_3^(2-)# is given by:
#nCO_3^(2-)=20.00xx0.10/1000=2.00xx10^(-3)#
At #0.05"ml"# before the end-point we have added #19.05"ml"# of #0.10"M"color(white)xHCl"_((aq))#.
The number of moles of #HCl# added is given by:
#nHCl=19.05xx0.10/1000=1.905xx10^(-3)#
This will be equal to the number of moles of #HCO_3^-# formed.
So the number of moles of #CO_3^(2-)# remaining is given by:
#nCO_3^(2-)=(2.00xx10^(-3)-1.905xx10^(-3))=0.095xx10^(-3)#
To get the number of moles of #H^+# released we can use an ICE table based on #"mol/l"#
#color(white)(xxx)HCO_3^(-)color(white)(xxxxx)rightleftharpoonscolor(white)(xxxx)CO_3^(2-)color(white)(xxxxx)+color(white)(xxxxx)H^+#
#color(red)"I"color(white)(xxx)1.905xx10^(-3)color(white)(xxxxxx)0.095xx10^(-3)color(white)(xxxxxxxx)0#
#color(red)"C"color(white)(xxxx)-xcolor(white)(xxxxxxxxxxxxxx)+xcolor(white)(xxxxxxxxx)+x#
#color(red)"E"color(white)(xxx)(1.905xx10^(-3))-xcolor(white)(xxx)(0.0905xx10^(-3))+xcolor(white)(xx)x#
Since #x# is much smaller than #nHCO_3^-# and #nCO_3^(2-)# we can say that at equilibrium:
#:.nHCO_3^(-)=(1.905xx10^(-3))-xrArr(1.905xx10^(-3))#
and:
#nCO_3^(2-)=(0.095xx10^(-3))+xrArr(0.095xx10^(-3))#
I will make this approximation in the rest of the calculations.
The expression for #K_(a2)# is:
#K_(a2)=([CO_3^(2-)][H^+])/[[HCO_3^-]]#
Since the total volume is common to all species we can write:
#:.[H^+]=4.68xx10^(-11)xx(1.905xxcancel10^(-3))/(0.095xxcancel(10^(-3))#
#:.[H^(+)]=9.38xx10^(-10)#
#:.pH=-log(9.38xx10^(-10))#
#color(red)(pH=9.02#
This represents the pH just before the 1st end-point.
(B)
At the end-point the 1st protonation is complete:
#CO_3^(2-)+H^(+)rarrHCO_3^-#
So we now have #40.00"ml"# of a solution containing #2.00xx10^(-3)# moles of #HCO_3^-# ions.
As we continue to add acid the 2nd protonation starts to happen:
#HCO_3^(-)+H^+rarrH_2CO_3#
After the end point at #20.00"ml"# we add #0.05"ml"# of #0.1"M"color(white)(x)"HCl"#:
The number of moles of #H^+# added is given by:
#nH^+=0.05xx0.10/1000=5.00xx10^(-6)#
From the equation of the reaction for this stage of the titration we can say that:
#nH_2CO_3# formed #=5.00xx10^(-6)#
So the number of moles of #HCO_3^-# remaining is given by:
#nHCO_3^(-)=(2.00xx10^(-3))-(5.00xx10^(-6))=0.001995#
#K_(a1)=([HCO_3^-][H^+])/([H_2CO_3])#
#:.[H^+]=K_(a1)xx([H_2CO_3])/([HCO_3^-])#
#:.[H^+]=4.27xx10^(-7)xx(5.00xx10^(-6))/(0.001995)=1.0675xx10^(-9)#
#:.pH=-log(1.0675xx10^(-9))#
#color(red)(pH=8.97)#
Phenolphthalein is an indicator that changes colour over the pH range 8.3 - 10 so is a suitable indicator for this end-point.
(C)
Now the titration continues to #0.05"ml"# short of the 2nd end-point which occurs at #40.00"ml"# of #"HCl"# added.
Since the 1st end-point we have added #19.05"ml"# of #0.10"M"color(white)(x)" HCl"#.
#:.nH^+# added #=19.05xx0.10/1000=1.905xx10^(-3)#
#:.nH_2CO_3# formed #=1.905xx10^(-3)#
#:.nHCO_3^-# remaining = #(2.00xx10^(-3))-(1.905xx10^(-3))=0.095xx10^(-3)#
#K_(a1)=([H^+][HCO_3^-])/([H_2CO_3])#
#:.[H^+]=K_(a1)xx[[H_2CO_3]]/[[HCO_3^(-)]]#
#:.[H^+]=4.27xx10^(-7)xx(1.905xxcancel(10^(-3)))/(0.095xxcancel(10^(-3)#
#[H^+]=8.561xx10^(-6)#
#pH=-log(8.561xx10^(-6))#
#color(red)(pH=5.06)#
(D)
When we get to the end point this reaction has reached completion:
#Na_2CO_(3(aq))+2HCl_((aq))rarrH_2CO_(3(aq))+2NaCl_((aq))#
So we have # 60"ml"# of a solution that contains #2xx10^(-3)# moles of #H_2CO_3#.
We can find the pH of this solution. I will ignore the 2nd ionisation because #K_(a2)# is much smaller than #K_(a1)#.
#K_(a1)=([HCO_3^-][H^+])/([H_2CO_3])#
Since #[H^+]=[HCO_3^-]# we can write:
#[H^+]^(2)=K_(a1)xx[H_2CO_3]#
We can find #[H_2CO_3]# using #c=n/v:#
#[H_2CO_3]=(2.00xx10^(-3))/(60.00/1000)=0.033"mol/l"#
#:.[H^+]^2=4.27xx10^(-7)xx0.033#
#[H^+]^2=1.41xx10^(-8)#
#:.[H^+]=1.187xx10^(-4)"mol/l"#
#pH=-log(1.187xx10^(-4)) #
#pH=3.92#
Now we add an extra #0.05"ml"# of # 0.1"M"color(white)(x)" HCl"#. The extra number of moles of #H^+# added is given by:
#0.10xx0.05/1000=5.00xx10^(-6)#
The number of moles of #H^+# which are already there due to the dissociation of #H_2CO_3# is given by:
#n=cxxv=1.187xx10^(-4)xx60.00/1000=7.122xx10^(-6)#
So we add this to the extra #H^+# added to get the total moles of #H^(+)# present:
#nH^(+)=(7.122+5)xx10^(-6)#
#nH^(+)=1.2122xx10^(-5)#
The new total volume is #60.05"ml".#
#:.[H^+]=(1.2122xx10^(-5))/(60.05/1000)=2.00xx10^(-4)"mol/l"#
#pH=-log(2xx10^(-4))#
#color(red)(pH=3.7)#
So you can see the pH has dropped slightly.
I have ignored any #H^+# from the ionisation of water.
The pH curve looks like this:
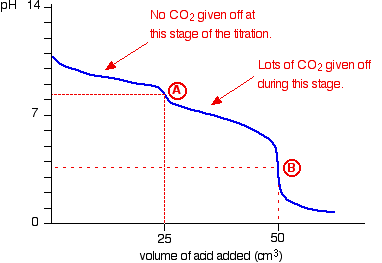
(In our example A is at 20.00ml, B is at 40.00ml)
Methyl Orange is an indicator which changes colour over the range pH 3.1 - 4.4 so is suitable for this end-point.
*


