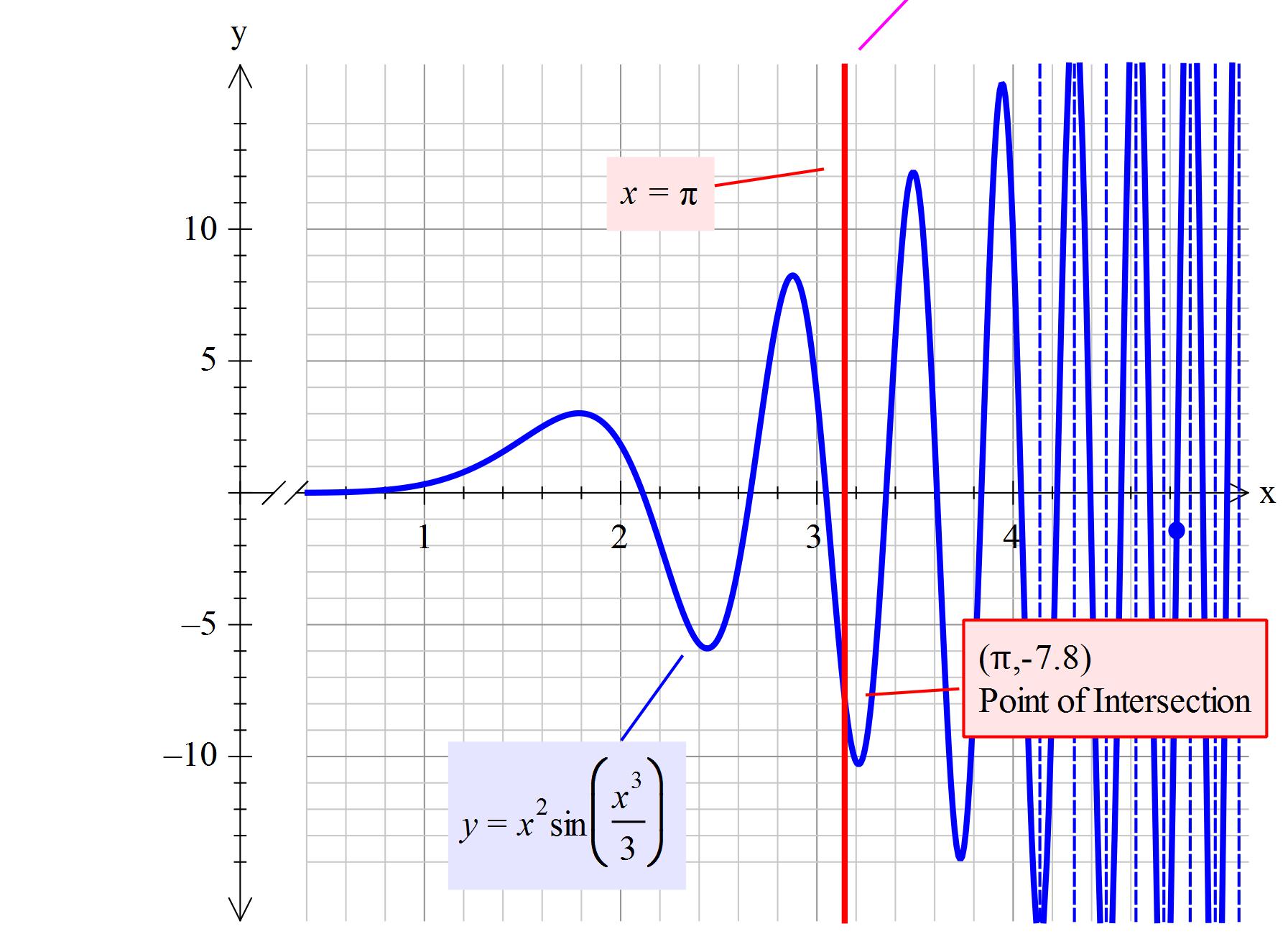
Let #f(x)=y=x^2sin(x^3/3)#
Let #u=x^2 =>color(brown)( (du)/dx=2x)#
Let #w=x^3/3=> color(brown)( (dw)/dx=(3x^2)/3 = x^2)#
Let #v=sin(w)=> color(brown)((dv)/dx)=(dv)/(dw) *(dw)/(dx) = x^2cos(w) color(brown)(= x^2cos((x^3)/3))#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using :#" "(dy)/(dx)=v (du)/(dx)+u (dv)/(dx)#
#=> (dy)/(dx)= sin(w)*2x+x^2*x^2cos(w)#
#=> (dy)/(dx)= 2xsin((x^3)/color(red)(2))+x^4cos((x^3)/3) color(red)("Found the error!")#
#=> (dy)/(dx)= 2pisin((pi^3)/color(magenta)(3))+pi^4cos((pi^3)/3)" "color(magenta)("Corrected"#
'~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Consider "2pisin((pi^3)/3)#
#pi^3/3 ~~ 10.3345" radians "-> 1.645" revolutions "-= 232.176^o#
So#" "color(brown)(2pisin(pi^3/2) ~~-4.9631 " 4dp") color(magenta)(" Corrected")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Consider "pi^4cos(pi^3/3))#
#pi^3/3 ~~10.3354" radians " -> 1.6449" revolutions " -= 232.176^o #
So#" "color(brown)(pi^4cos(pi^3/3)~~ -59.7346#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)(=>(dy)/(dx)= -64.6977" "color(magenta)(" Corrected - Tony B"#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the equation of the tangent")#
Derived the gradient as -64.6977 to 4 decimal places
Thus #y=mx+c" "->" "y=(-64.6977)x+c#...........................(1)
Need to establish a point coordinate so that #y=mx+c# can be resolved.
#color(brown)(underline("Determine value of y at "x=pi))#
At #x=pi#
# y=x^2sin(x^3/3) -> pi^2*sin(pi^3/3)#
Consider #sin(pi^3/3)#
The #pi^3/3# is a count of radians and there are #2pi# radians in a complete cycle
So #pi^3/3 ~~10.33" radians"#
This is #~~ 10.33/(2pi)" full cycles" ~~1.644#
For reference #0.644" cycles "~~232.176^o#
So #color(brown)(y=pi sin(pi^3/3) ~~pi sin(232.176)~~-7.899)# to 3 dp
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So equation (1) becomes #("at "x=pi#)
#y=mx+c" "->" "-7.899=(-64.6977)pi+c#
#=> c~~-7.899+(64.6977)pi#
#=>c~~195.355# to 3 dp
Thus the equation of the tangent is
#color(blue)(y~~(-64.6977)x+195.355)# to 3 dp


