A medical researcher says that less than #25%# of US. adults are smokers. In a random sample of #200# US. adults, #18.5%# say that they are smokers. At #alpha = 0.05#, is there enough evidence to reject the researchers claim?
1 Answer
The medical researcher's expectation is wrong. There is enough statistical evidence to prove that 25% or more are smokers in the university.
Explanation:
It is about testing the significance of sample Proportions.
Population Parameter
P = 25% [Population Proportion}
Sample Statistic
p=18.5% [sample Proportions]
Significance level 0.05
Sample size
Distribution to be used : Normal Distribution [since
#H_O:P>=25%#
#H_1:P<25%#
[Tips : We are going to compare Calculated
Calculations:
Table Value (
In our case table value is
Since left tail test is used the actual Table value is
Refer the image.
Calculated
Here
#SE=sqrt(200 xx 0.25 xx 0.75)=6.124#
#z=(18.5-25)/6.124=(-6.5)/6.124=-1.06#
Conclusion:
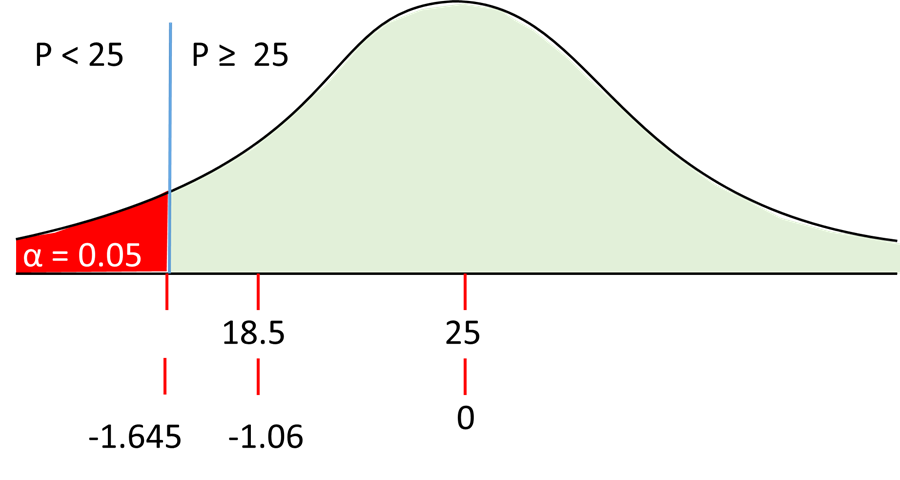
Since the calculated value
Inference:
There is enough statistical evidence to prove that 25% or more are smokers in the university.
It means, the medical researcher's expectation is wrong.

