An object has a mass of 4 kg. The object's kinetic energy uniformly changes from 144 KJ to 124KJ over t in [0, 6 s]. What is the average speed of the object?
4 Answers
I found:
Explanation:
From your Kinetic Energies you can work out the speed (at two instants of time) knowing that kinetic energy
so, rearranging:
Now we use the kinematic relationship:
to get:
and:
and the other relationship:
The average speed during your time interval will then be:
ALTERNATIVE
If Eq(2) is divided by Eq (1) we get
av velocity
If Initial velocity be u m/s and final velocity v m/s after 6 s
then
Again
average speed for uniform change in velocity( i.e. having uniform retardation) =
If uniform change in KE with time is considered then calculation will not match with this one
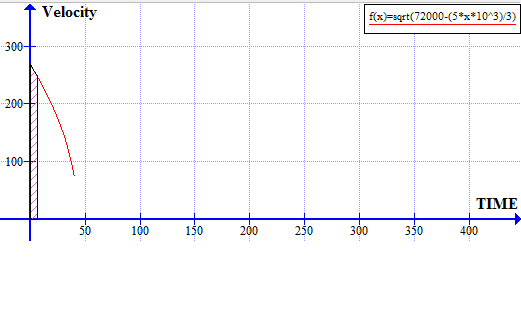
From the graph
Explanation:
It is given that the Kinetic energy changes uniformly.
We know that
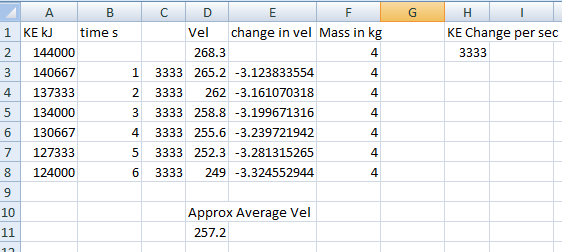
Divide the given change in velocity by
Calculate velocities at time
Observe that the change in velocity in each second interval is not constant. As such, acceleration is not constant. Therefore, the known expressions for linear motion for constant acceleration can not be applied.
I have attempted to assess Approx Average velocity by calculating distance moved in each second. This is approximately equal to the velocity for that second. Take the sum of these six distances and divide by time that is
More accurately, one should draw a
Area Graph added
~~258.8m/s#
Explanation:
Initial KE
After 6s Final KE
KE is uniformly decreased, so it will have a constant negative slope
and this slope will be
If at t th instant
We are to find out a relation between v and t
the KE at t th instant
Now
Now distance traversed during 6 s
Let
when
when
Hence the average speed