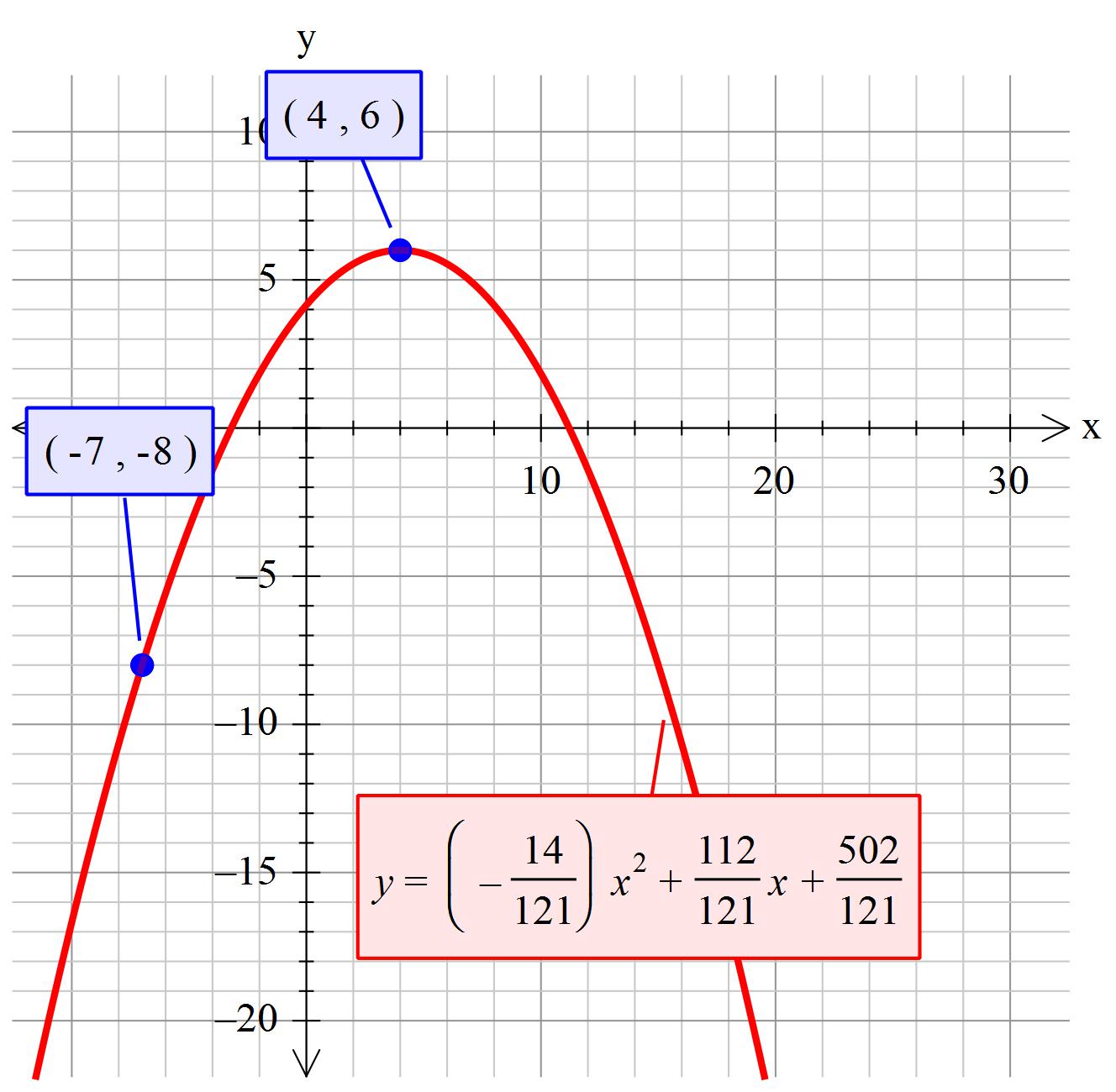
What is the equation of the parabola that has a vertex at # (4, 6) # and passes through point # (-7,-8) #?
2 Answers
Explanation:
Known: The equation standard form is
Using the two points to give simultaneous equations
Known that
So
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In vertex form:
#y = -14/121 (x-4)^2 + 6#
In standard polynomial form:
#y =-14/121 x^2 + 112/121 x +502/121#
Explanation:
The equation of a parabola with vertical axis can be expressed in vertex form as:
#y = a(x - h)^2 + k#
where
In our example, the equation of the parabola can be written in the form:
#y = a(x - 4)^2 + 6#
from which we can deduce:
#a = (y-6)/(x-4)^2#
Since we want our parabola to pass through
#a = (-8-6)/(-7-4)^2 = -14/121#
So the equation of our parabola may be written:
#y = -14/121 (x-4)^2 + 6#
#=-14/121 x^2 + 112/121 x - 224/121 + 6#
#=-14/121 x^2 + 112/121 x +502/121#
graph{-14/121 x^2 + 112/121 x +502/121 [-20, 20, -10, 10]}


