We start from the given equation f(x)=cos x-e^x sin x
Let us solve for the point of tangency first
f(pi/3)=cos (pi/3)-e^(pi/3) sin (pi/3)
f(pi/3)=1/2-e^(pi/3) sqrt(3)/2
Let us solve for the slope m now
f(x)=cos x-e^x sin x
Find the first derivative first
f' (x)=d/dx(cos x-e^x sin x)
f' (x)=-sin x-[e^x*cos x+sin x*e^x*1]
Slope m=f' (pi/3)=-sin (pi/3)-[e^(pi/3) cos (pi/3)+sin (pi/3)*e^(pi/3)]
m=f' (pi/3)=-sqrt(3)/2-[e^(pi/3) *1/2+sqrt(3)/2*e^(pi/3)]
m=f' (pi/3)=-sqrt(3)/2-[1/2+sqrt(3)/2]*e^(pi/3)
m=f' (pi/3)=-1/2[sqrt(3)+e^(pi/3)+sqrt(3)e^(pi/3)]*
Our Tangent Line:
y-f(pi/3)=m(x-pi/3)
y-1/2+ sqrt(3)/2*e^(pi/3)=-1/2(sqrt(3)+e^(pi/3)+sqrt(3)e^(pi/3))(x-pi/3)
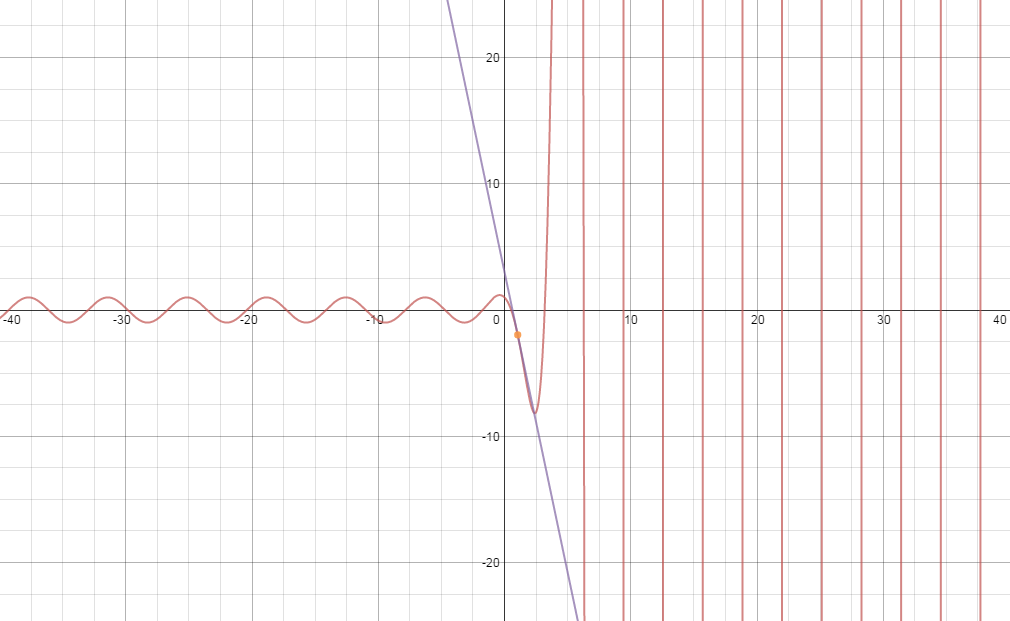
Kindly see the graph of f(x)= cos x-e^x sin x and the tangent line
y-1/2+ sqrt(3)/2*e^(pi/3)=-1/2(sqrt(3)+e^(pi/3)+sqrt(3)e^(pi/3))(x-pi/3)
God bless....I hope the explanation is useful.

