A cone has a height of #18 cm# and its base has a radius of #5 cm#. If the cone is horizontally cut into two segments #12 cm# from the base, what would the surface area of the bottom segment be?
1 Answer
Explanation:
Lets first consider the cross-section of the cone.
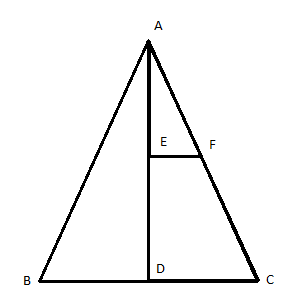
Now it is given in the question, that AD =
given, DE =
Hence, AE =
As,
After cutting, the lower half looks like this:
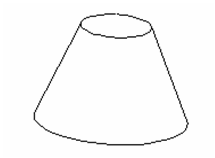
We have calculated the smaller circle (the circular top), to have a radius of
Now lets calculate the length of the slant.
The surface area of the whole cone is :
Using the similarity of the triangles
So the slant surface area of the upper part (the smaller cone) is :
Hence of the slant surface area of the lower part is:
And we have the the upper and lower circular surfaces' areas as well.
So the total area is: