Example 1 You can work this one out without using calculus
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Example using Calculus from first principles")#
Suppose we wish to find the generic equation of the tangent for any point on the curve #color(blue)(y=x^2+2x+3)#
The gradient (tangent) is:#" "("Change in y-axis")/("Change in x-axis")#
But this is calculated for a minute change that is so small you can not see it.
#color(green)("Let the minute change in "x" be "delta x)#
If #x# has changed then so will #y#
#color(green)("Let the minute change in "y" be "deltay)#
Then :#" "("Change in y-axis")/("Change in x-axis")= (delta y)/(delta x)#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So after the change the original equation becomes:
#color(blue)(y=x^2+2x+3)color(brown)(" " ->" " (y+ delta y)=(x+ delta x)^2+2(x+delta x)+3)#
Multiply out the brackets giving:
#y+ delta y" "=" "x^2+2xdelta x +(delta x)^2+2x+2delta x+3#
Reordering the terms:
#color(green)(color(blue)(y)+ delta y" "=" " color(blue)(x^2+2x+3)+2xdelta x+2delta x+(delta x)^2)#
Subtract the original equation
#color(green)(delta y=2xdelta x+2delta x+(delta x)^2)#
Divide both sides by #delta x#
#color(green)((delta y)/(delta x)=2x(delta x)/(delta x)+2(delta x)/(delta x)+((delta x)^2)/(delta x)#
But #(delta x)/(delta x) = 1# giving:
#color(green)((delta y)/(delta x)=2x+2+delta x#
Suppose #delta x# gets so small that it may as well be 0 then we have
#color(green)((delta y)/(delta x)=2x+2 ->("Change in y-axis")/("Change in x-axis") " "=" "m#
#color(red)("This is the gradient of the tangent for any point.")#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The tangent is a straight line #->y=color(red)(m)x+c#
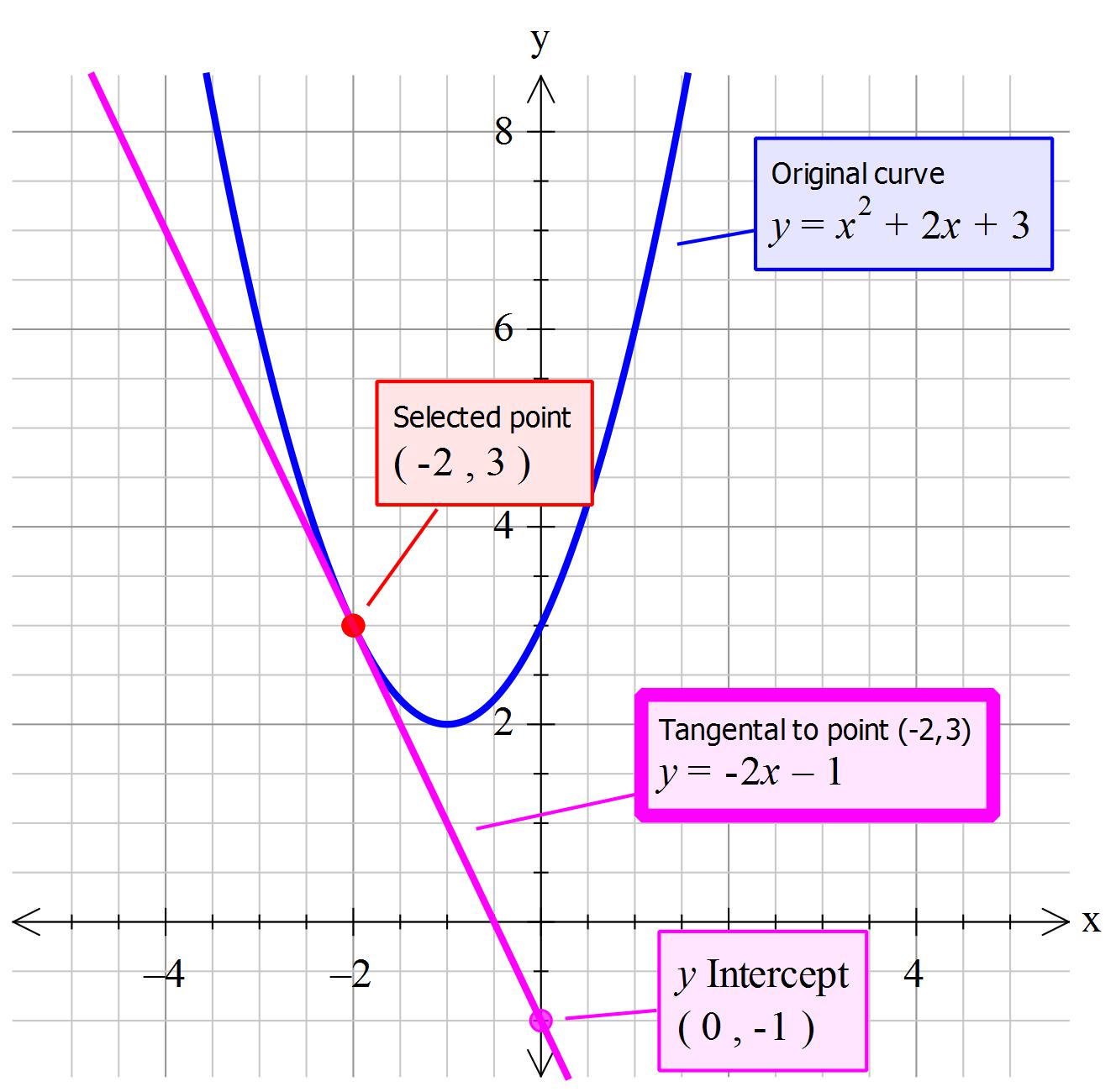
Suppose we had the point on the curve of #(-2,3)# then the
Then #color(red)(m->2x+2" " =" " 2(-2)+2=-2#
Thus:#" "y=color(red)(m)x+c->y=color(red)(-2)x+c#
But it passes through the point #(x,y)->(-2,3)# giving
#y=color(red)(-2)x+c" " ->" "3=color(red)(-2)(-2)+c#
#=>c=-1#
#y=color(red)(-2)x-1#



