Question

A projectile is launched with an initial speed of Vo at an angle θ above the horizontal. It lands at the same level from which it was launched. What was the average velocity between launch and landing? Explain please because I can't understand this.

Answer 1

`"Average velocity"=V_@ cos theta`

Explanation:

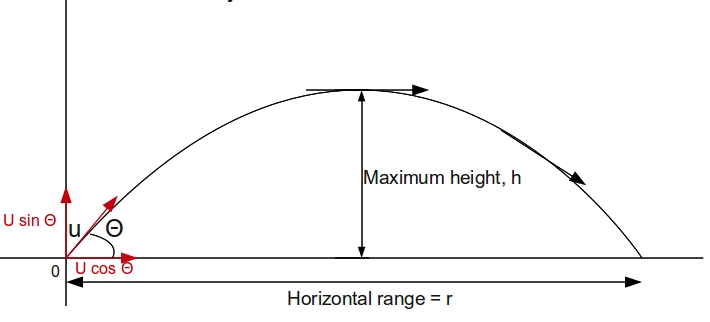
Typical flight of a projectile is as shown in the picture above.
In the problem it is given that initial velocity `V_@` at an angle `theta` above the horizontal. As such inn the picture `"U"=V_@`.

This velocity can be resolved into its `x and y` components.
Component along `x` axis, and
Component along `y` axis`=V_@ sin theta`

We also know that both `x and y` components are orthogonal or perpendicular to each other, therefore can be treated separately.

Maximum height is achieved due to `sin theta` component of the velocity and Horizontal range is achieved due to `cos theta` component.

`sin theta` component.
This component of the velocity decreases due to action of gravity. Becomes zero at the maximum height point. Then increases due to gravity and becomes equal to initial `sintheta` component but in the opposite direction. We have ignored the friction due to air (Drag) acting on the projectile.
Let `t` be time of flight.
`"Average velocity"="Displacement"/"Time of flight"`

It is given that "It lands at the same level from which it was launched", means that displacement in the `y` axis is `=0`. From above equation we obtain
`"Average velocity"=0/t=0` .....(1)

`cos theta` component.
If we ignore air resistance, `cos theta` component of velocity `=V_@ cos theta` remains constant throughout the time of flight. Therefore,
`"Average velocity"=V_@ cos theta` .....(2)

Now to find the Resultant Average velocity we need to add both vectors along `x and y` direction. In this instant it is simple as one of the vectors is `=0`.

Hence, `"Average velocity"=V_@ cos theta`