Question

Let the random variables X and Y have the joint pmf `f(x,y)=(x+y)/32`, `x=1,2`, and `y=1,2,3,4`. What are the means `mu_x` and `mu_y`, the variances `sigma ""_x^2` and `sigma "" _y^2`, and the correlation coefficient `rho`?

Answer 1

`mu_x=1.5625`
`mu_y=2.8125`
`sigma_x^2=0.24609375`
`sigma_y^2=1.15234375`
`rho approx -0.0366766`

Explanation:

Let's calculate those joint probabilities:

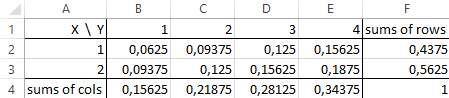
e.g. `P(X=2 wedge Y=3)=0.15625`.
It is now quite easy to obtain separate probability distributions of `X` and `Y`: we should sum rows or columns of area B2:E3, respectively, e.g.
`P(X=2)=sum_(i=1)^4 P(X=2 wedge Y=i)=0.09375+ldots+0.1875=0.5625`
Now we can use known formulas for the values we're looking for:
`mu_x="E"X=1*0.4375+2*0.5625=1.5625`
`mu_y="E"Y=1*0.15625+2*0.21875+3*0.28125+4*0.34375=2.8125`
`"E"X^2=1^2*0.4375+2^2*0.5625=2.6875`
`"E"Y^2=1^2*0.15625+ldots+4^2*0.34375=9.0625`
`sigma_x^2="E"X^2-"E"^2X=2.6875-1.5625^2=0.24609375`
`sigma_y^2="E"Y^2-"E"^2Y=9.0625-2.8125^2=1.15234375`

Now for the correlation coefficient `rho` we need the covariance `sigma_(xy)` so let's find the probability distribution of `XY`: (here `p_(ij)=P(X=i wedge Y=j)` )

`P(XY=1)=p_(11)=0.0625`
`P(XY=2)=p_(12)+p_(21)=0.1875`
`P(XY=3)=p_(13)=0.125`
`P(XY=4)=p_(14)+p_(22)=0.28125`
`P(XY=5)=0`
`P(XY=6)=p_(23)=0.15625`
`P(XY=7)=0`
`P(XY=8)=p_(24)=0.1875`

Now, for the covariance:
`"E"(XY)=1*0.0625+ldots+8*0.1875=4.375`
`sigma_(xy)="E"(XY)-"E"X*"E"Y=-0.01953125`
`rho=(sigma_(xy))/sqrt(sigma_x^2*sigma_y^2)=-0.0366765706779718`