Question

A cone has a height of `6 cm` and its base has a radius of `6 cm`. If the cone is horizontally cut into two segments `3 cm` from the base, what would the surface area of the bottom segment be?

Answer 1

Yosief you answer is great but you just subtracted the original cone and the top cone. While that will give you a complete solution for the volume for the surface area you have three parts you need to consider:
1) The Base Area => this area of the circle
2) The side Area, that is the one you got by `pis(R-r)` that you have right
3) Because you cut it now you have a smaller circle on top so you need to this area.

So using your terms
`SA_F = "BA + Side Area + Top Area"`
`SA_F = piR^2 + pis(R-r) + pir^2 = pi(R^2+r^2) + pis(R-r)`

What changed? Well in your formula the first is the sum of squares instead the difference of squares. You were not that far you were a sign away from the correct answer. Make that change and voila you got it...

Answer 2

Surface area of bottom shape = `9pi(4 + sqrt18)`

Explanation:

Let's start off by writing down what is already known and then finding some of the values we will need later.

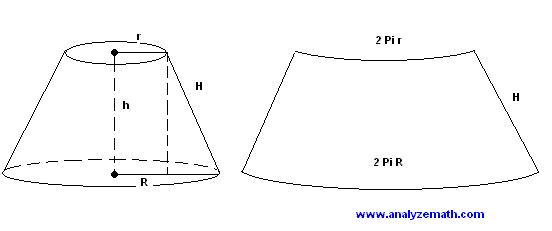
The BIG cone and the small cone are similar figures.
R = 6cm ; r = 3cm
H = 6cm ; h = 3cm
L = `sqrt72` ; `l` = `sqrt18` (`l` is the slant height, found by Pythagoras)

Small cone:
surface area = area base + curved surface
s.a. = `pi r^2` + `pi r l` = `pi(3)^2 + pi (3)sqrt18`

Factorise to make it easier: s.a. = `3pi(3 + sqrt18)`

In similar figures, the areas are in the same ratio as the square of the sides, length, radius etc.

`3^2/6^2` = `(3pi(3 + sqrt18))/(SA)` `rArr` `1/4` = `(3pi(3 + sqrt18))/(SA)`

BIG CONE: Surface area = `4 xx 3pi(3 + sqrt18)`
= `12pi(3 + sqrt18)`

Surface area of fustrum (bottom segment);

BIG AREA - small area

= `12pi(3 + sqrt18)` - `3pi(3 + sqrt18)`

= `9pi(3 + sqrt18)`

However, the circular cut surface must be included as well.

Total Surface area = `9pi(3 + sqrt18)` + `pi(3)^2`
= `9pi(3 + sqrt18)` + `9pi`
= `9pi(3 + sqrt18 +1)`
= `9pi(4 + sqrt18)`