Question

What is the limit of `(1 + 2/x)^x` as x approaches infinity?

Answer 1

`lim_(xrarroo)(1+2/x)^x = e^2`

Explanation:

Use `lim_(urarroo)(1+1/u)^u = e`

`lim_(xrarroo)(1+2/x)^x = lim_(xrarroo)(1+1/(x/2))^x`

`= lim_(xrarroo)((1+1/(x/2))^(x/2))^2`

`= (lim_(xrarroo)(1+1/(x/2))^(x/2))^2`

Now we have the form above with `u = x/2`, so we evaluate the limit.

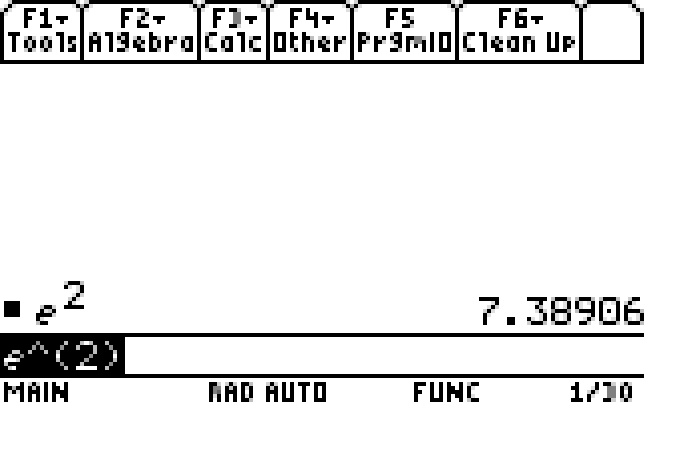
`= e^2`

Answer 2

Jim, awesome ..

What this limit really represents is essentially the horizontal asymptote y = `e^2`, reflecting the function's long term graphical behavior.

Explanation:

Here are a couple of TI screenshots showing the graph and the decimal expansion for `e^2`.

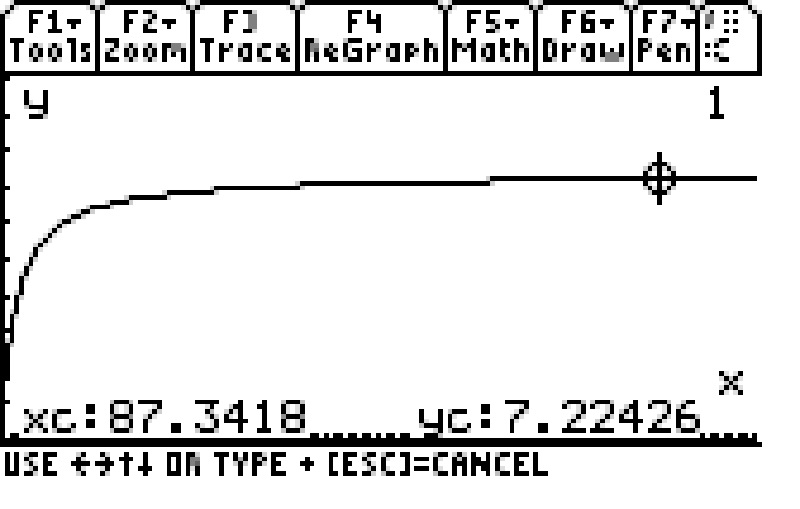
If we went even further out to the right and then asked some random guy on the street if they are looking at a straight line, they would say "yes!".

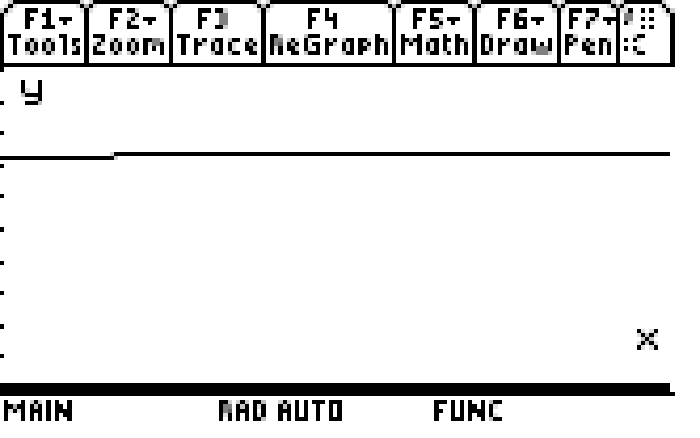
But in fact you are looking at the curve endowed with concavity, not a straight line. The curve is asymptotically approaching the value of `y=e^2`