How do you prove that the function #g(x) = x^3 / x# is continuous everywhere but x=0?
1 Answer
You must prove that the limit of the function exists everywhere, accept to
Explanation:
There are several ways to prove continuity, they differ in key ideas and mathematical formality.
The function f is continuous at some point c of its domain if the limit of f(x) as x approaches c through the domain of f exists and is equal to f(c). In mathematical notation, this is written as
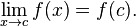
In detail this means three conditions: 1) first, f has to be defined at c. 2) Second, the limit on the left hand side of that equation has to exist. 3) Third, the value of this limit must equal f(c).
For our function:
Nonetheless, as you can see from the graph below, this function is continuous on 0 , since
But the ideas herein can be used to prove that a true not continuous function is not continuous in a point, e.g.
graph{x^3/x [-2.5, 2.5, -1.25, 1.25]}
See for more details:
https://en.wikipedia.org/wiki/Continuous_function#Definition_in_terms_of_limits_of_functions

