Question

Question #3f1d8

Answer 1

If a man is standing by the track and train is running at `60` `km`/`hr` to south his relative velocity is `60` miles south direction.

Explanation:

If he is also running at `10` `km`/`hr` towards south, his velocity relative to train is only `60-10` = `50` `km`/`hr` to south.

If he run to north at `10` `km`/`hr` his relative velocity will be `70` `km`/`hr` with train.
Hope this explains the relative velocity.

Answer 2

Concept.
For rain problem,
If `vecV_A and vecV_B` are velocities of objects `A and B` respectively then

`vecV_(AB)=vecV_A-vecV_B` is the velocity of `A` with respect to `B`.

Explanation:

Following the above logic

`vecV_(rm)=vecV_r -vecV_m` is velocity of rain with respect to man.

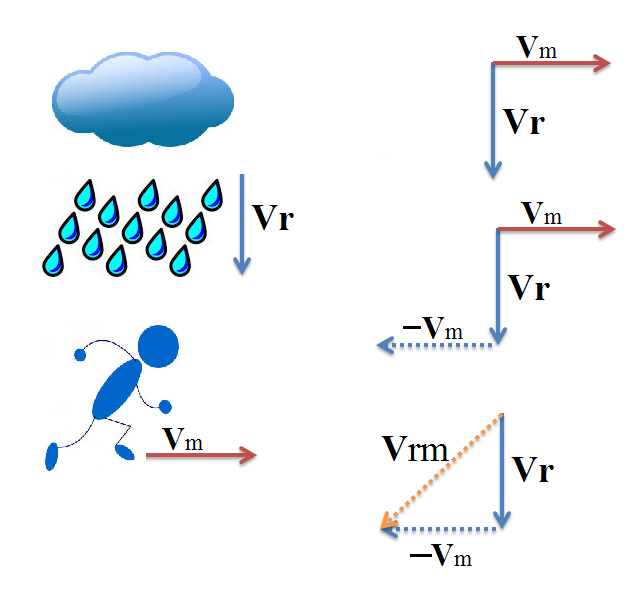
See the vector representation on the right side of the figure above.

1. Velocity vectors `vecV_m and vec V_r` are drawn.
2. Recall `-ve` sign in front of the the second term.
   Therefore, draw `-vecV_m` at the tip of `vecV_r`
3. Join the tail of `vecV_r` to the tip of `-vecV_m` to obtain `vecV_(rm)` as velocity of rain with respect to man.

Similar steps need to be followed if `vecV_(mr)`, velocity of man with respect to rain is to be found.

1. Velocity vectors `vecV_m and vec V_r` are drawn.
2. We are to find out `vecV_(mr)`, velocity of man with respect to rain.
   We know that `vecV_(mr)=vecV_m-vecV_r`
   Therefore draw `-vecV_r` at the tip of `vecV_m`
3. Join the tail of `vecV_m` to the tip of `-vecV_r` to obtain `vecV_(mr)` as velocity of man with respect to rain.