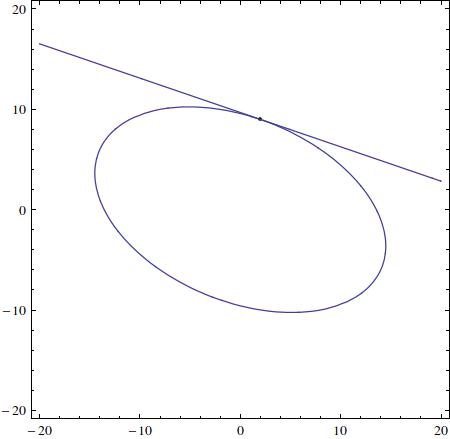
How do you find the equation of the line tangent to #x^2+xy+2y^2=184# at (x,y) = (2,9)?

Question

2380 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-05-26T14:47:16

#y = 9 -13/38(x-2)#

Given #f(x,y)=x^2+x y + 2y^2-184#
the tangent vector to any point #p=(x,y)#
such that #f(x,y)=0# is given by

#(dy)/(dx)=-(f_x)/(f_y)#

in our case we have

#(dy)/(dx) = -(2x+y)/(x+4y)#.

The given point #p_0=(2,9)# is such that #f(2,9)=0#.

In #p = p_0# we have #(dy)/(dx) = m = -13/38#.

The tangent line to #f(x,y)# in #p_0# is giving by

#y = 9 -13/38(x-2)#

enter image source here