Question

A cone has a height of `27 cm` and its base has a radius of `12 cm`. If the cone is horizontally cut into two segments `8 cm` from the base, what would the surface area of the bottom segment be?

Answer 1

`1238.7cm^2`, rounded to one decimal place.

Explanation:

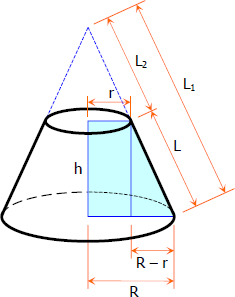
When we cut a right circular cone horizontally in two segments as in the problem, we end up with

1. A small cone (top part),
2. Frustum (bottom part).
   as shown in the above figure

The curved area of the frustum is given by the expression
Curved area of the frustum`=pi(R+r)L`
Area of the top circular face`=pir^2`
Area of the bottom circular face`=piR^2`
`:.`Total surface area of the frustum `=pi(R+r)L+pir^2+piR^2`
From the figure `L=sqrt(h^2+(R-r)^2)` .....(1)

To obtain `r` we use the proportionality theorem for similar triangles
`"Radius of larger cone"/"Radius of smaller cone"="Height of larger cone"/"height of smaller cone"`
or `12/r=27/(27-8)`
`=>r=12xx19/27=8.dot 4cm`
Inserting given values in (1) above we obtain
`L=sqrt(8^2+(12-8.dot 4)^2)`
`L=8.7545402682632041971077434799268`
Total surface area of the frustum `=pi(12+8.dot4)xx8.755+pi(8.dot4)^2+pi12^2`
`=562.288+224.023+452.389`
`=1238.7cm^2`, rounded to one decimal place.

-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-..-
Alternatively

We know that area of Curved surface of a right circular cone`=piRl`,
We can use this formula to calculate the curved surface of frustum

Curved surface of frustum`=`
Curved Surface of Larger Cone`-`Curved Surface of Smaller Cone