Consider the figure.
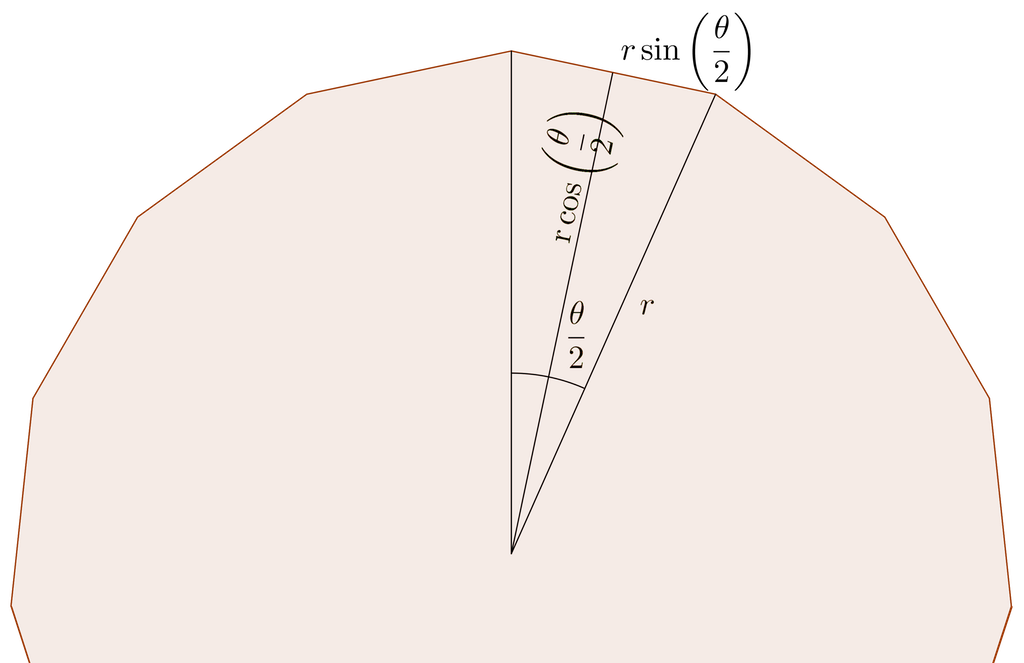
The sector delimited by two radius and a side is an isosceles triangle. If you cut in the middle that triangle you have two rectangle triangles.
The sides of that triangle are
#r, rsin(theta/2), rcos(theta/2)#
where #r# is the radius and #theta# is the angle of the initial triangle. That angle is simply the #2pi# divided by the number of sectors (or sides) of the polygon #n#.
#theta=(2pi)/n#
The area of the rectangle triangle is
#(rsin(theta/2)*rcos(theta/2))/2#
Consequently, the area of the isosceles triangle is
#2*(rsin(theta/2)*rcos(theta/2))/2#
#=rsin(theta/2)*rcos(theta/2)#
and in the polygon there are #n# of those isosceles triangles, so the area of the polygon is
#A=nrsin(theta/2)*rcos(theta/2)#.
We rearrange this formula to obtain something a bit nicer
#A=nr^2sin(theta/2)cos(theta/2)#
I use now the relationship
#sin(2\theta)=2sin(theta)cos(theta)# then
#sin(theta)=2sin(theta/2)cos(theta/2)# and
#sin(theta)/2=sin(theta/2)cos(theta/2)#. I substitute in the area obtaining
#A=nr^2(sin(theta))/2#
and finally I substitute the value of the angle #theta=(2pi)/n#
#A=nr^2(sin((2pi)/n))/2#
This is the searched formula. Now we can calculate the value substituting #r=13# mm and #n=15#, the result will be in #mm^2#.
#A=15*13^2(sin((2pi)/15))/2#
#A=15*13^2(sin((2pi)/15))/2\approx "515.54 mm"^2#.



