Question

How do you find the equation of the tangent line to the curve `y=sin(2x)` at x=pi/2?

Answer 1

Tangent line `y=-2x+pi`

Explanation:

Given `y=sin (2x)` at `x=pi/2`

solve for the point first

`y=sin (2x)`

`y=sin (2(pi/2))`

`y=0`

Our point `(x_1, y_1)=(pi/2, 0)`

Let us solve the slope m of the tangent line

`y=sin (2x)`

`y'=cos (2x)*d/dx(2x)=cos (2x)(2)=2*cos (2x)`

`m=2*cos (2(pi/2))=2*(-1)=-2`

`m=-2`

The Tangent Line

`y-y_1=m(x-x_1)`

`y-0=-2(x-pi/2)`

`y=-2x+pi`

Kindly see the graph of `y=sin (2x)` and `y=-2x+pi`

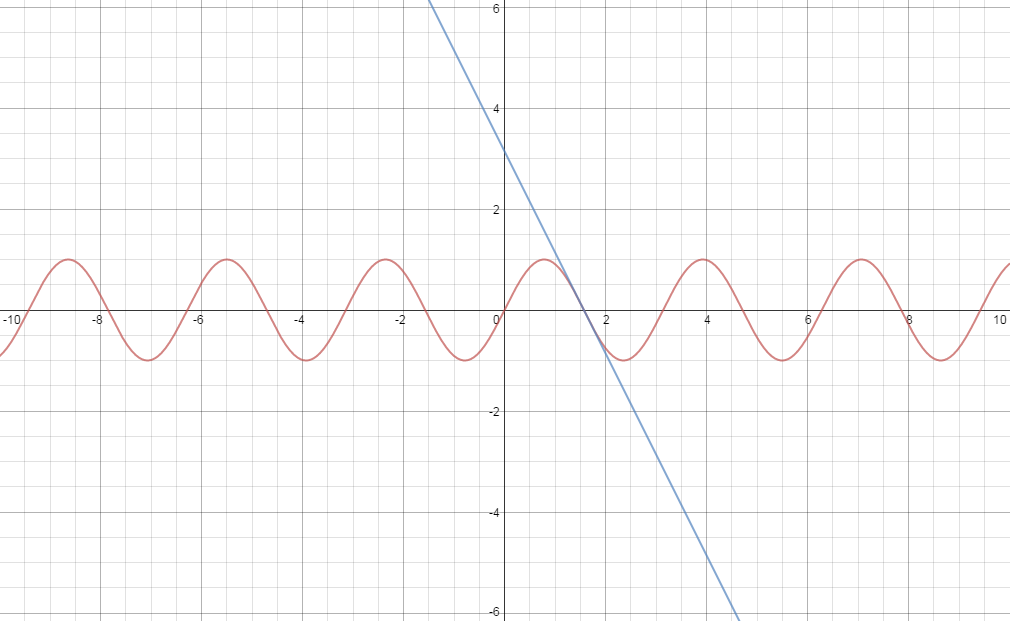
God bless....I hope the explanation is useful.