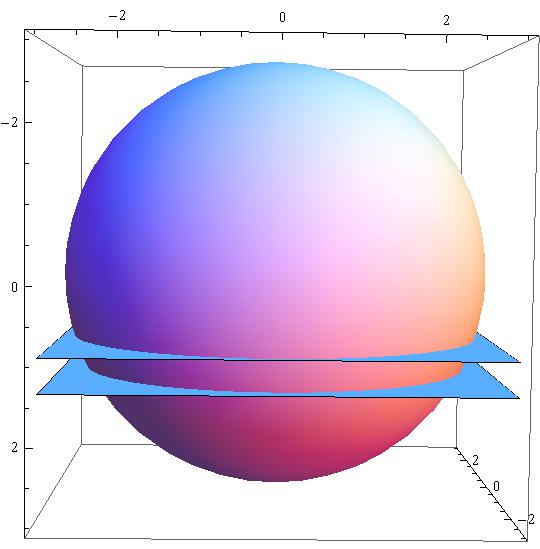
How do you find the volume of a solid where x^2+y^2+z^2=9 is bounded in between the two planes z+2x=2 and z+2x=3?
2 Answers
Explanation:
Cumbersome integration problems can be handled easily with the so called Monte Carlo method. https://en.wikipedia.org/wiki/Monte_Carlo_integration
This method works as follows.
1) Choose a box which contains the area/volume to be measured
2) Define the area/volume borders/restrictions
3) Generate inside the box, random values for the coordinates.
a) If for this point the restrictions are obeyed, consider this as a successful one
4)Given de box volume
In this case we have the restrictions defining the sought volume
A python program is attached showing the main details.
The result is

Explanation:
The present case can be simplified by a coordinate transformation.
Choosing the transformation
builded using one versor normal to the cutting planes
which are
The new system of coordinates
transform the original equations to
Calculating the revolution volume of
between the limits