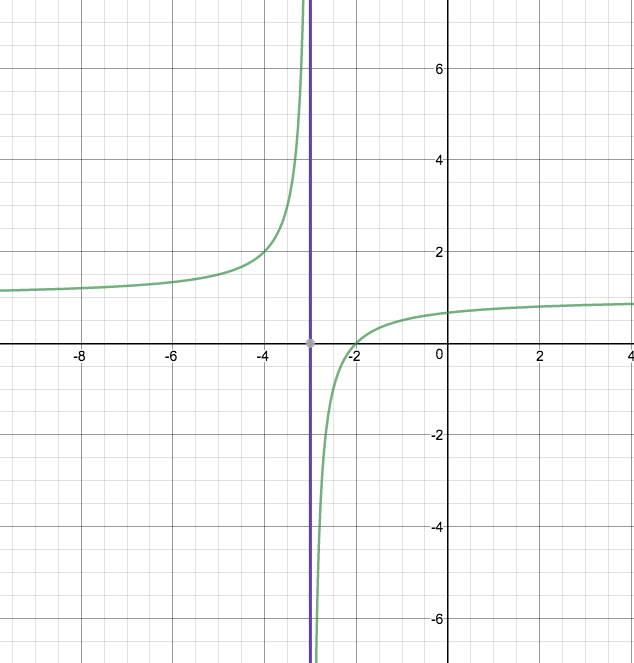
#lim_{x \to -3^+}(x+2)/(x+3)#
if we just plug in #x = -3#, we can see that it is #2/oo#. the graph shows that #lim_{x \to -3^+}(x+2)/(x+3) = - oo#
to see this, let #x = -3 + \epsilon# {ie just to right of x = -3], with #0 < \epsilon < < 1# we have
#(-3 + \epsilon + 2)/(-3 + \epsilon + 3)#
#= ( -1 + \epsilon )/(\epsilon)#
#= ( -1)/(\epsilon) + (\epsilon )/(\epsilon)#
#= -( 1)/(\epsilon) + 1#
we see that the dominant term for small #\epsilon# is #= -( 1)/(\epsilon) #, which is negative; and #lim_{\epsilon \to 0} -( 1)/(\epsilon) + 1 = -oo#