What is the derivative of #y = arccsc (x/2)#?

Question

4140 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-30T22:51:17

#- 2/(x sqrt(x^2 - 4))#

if #y = csc^{-1} (x/2)#

then

#csc y = x/2# [..... Which means that #color{red}{sin y = 2/x}#]

so

#D_x(csc y = x/2)#

#\implies - csc y \ cot y \ y ' = 1/2#

[#D_z (csc z) = - csc z cot z# is a well known derivative]

So we have
# y ' = 1/2 1/(- csc y \ cot y)#

#= - 1/2 sin y \ tan y#

the significance of the text in red is this:

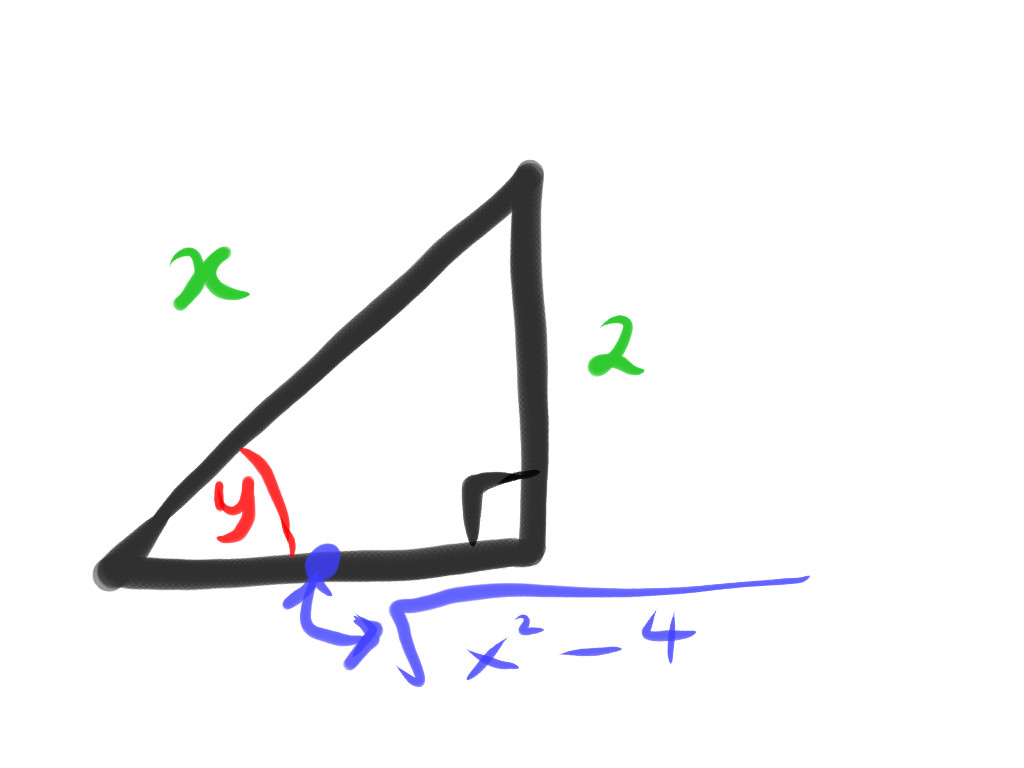
enter image source here

because it should be clear that #tan y = 2/sqrt(x^2 - 4)#

so

# y ' = - 1/2 * 2/x * 2/sqrt(x^2 - 4)#

# = - 2/(x sqrt(x^2 - 4))#