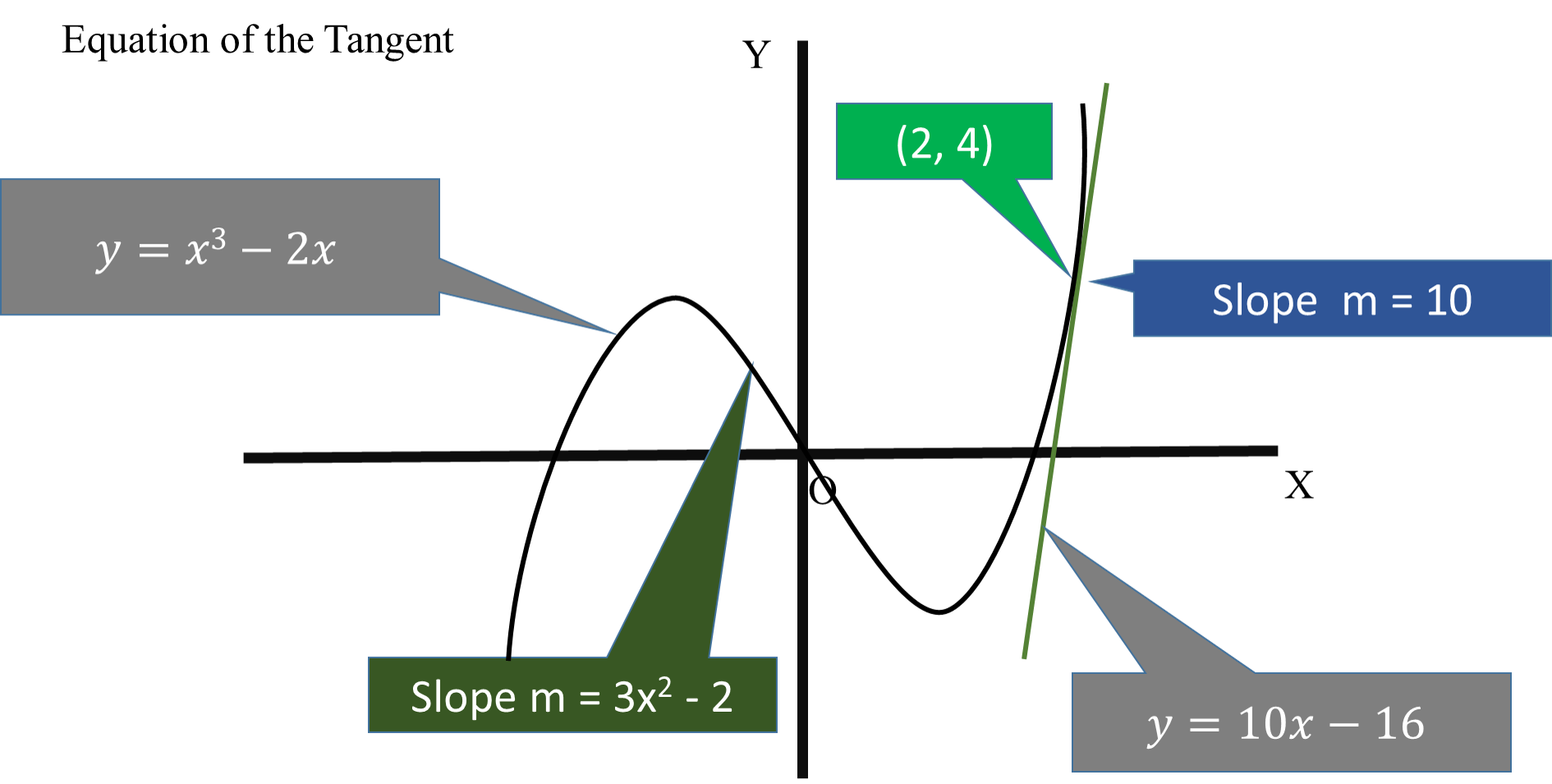
How do you find the equation of the tangent line to the curve #y=x^3 - 2x# at the point (2,4)?

Question

19140 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-02T07:18:34

#y=10x-16#

Given -
Curve is defined by the cubic function -

#y=x^3-2x#
Point #(2,4)# is on the curve

We have to know the slope of the curve at point #(2,4)#

Slope of the curve at any point on the curve is given by its first derivative.

#dy/dx=3x^2-2#

At #x=2# the slope is

#y=(3.(2^2)-2=12-2=10#

The equation of the tangent -

#c+mx=y#
#c+10.2=4#
#c=4-20=-16#

Then

#y=10x-16#

Look at the Figure