From a unit sphere, the part between two parallel planes equidistant from the center, and with spacing 1 unit in-between, is removed. The remaining parts are joined together face-to-face, precisely. How do you find the volume of this new solid?
2 Answers
Explanation:
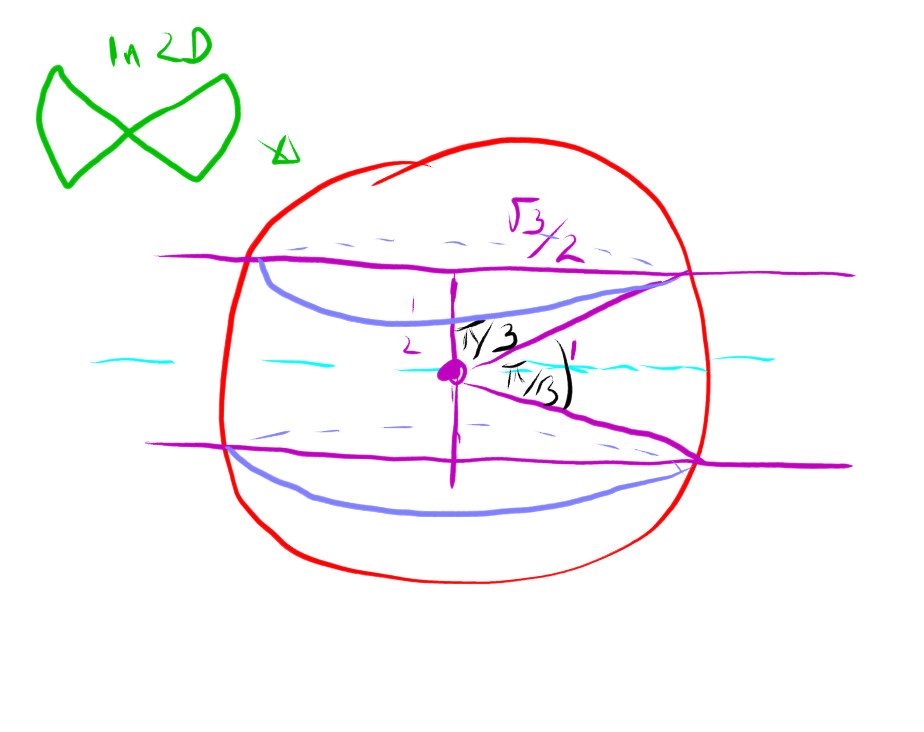
the bit you're removing can be seen to have 2 components. One that can be dealt with by spherical coords, as per the drawing. the green sketch in the top corner shows this in 2D. So the volume is that green wedge revolved about the z axis.
In addition, there are two cones, that are ommited by the spherical integration.
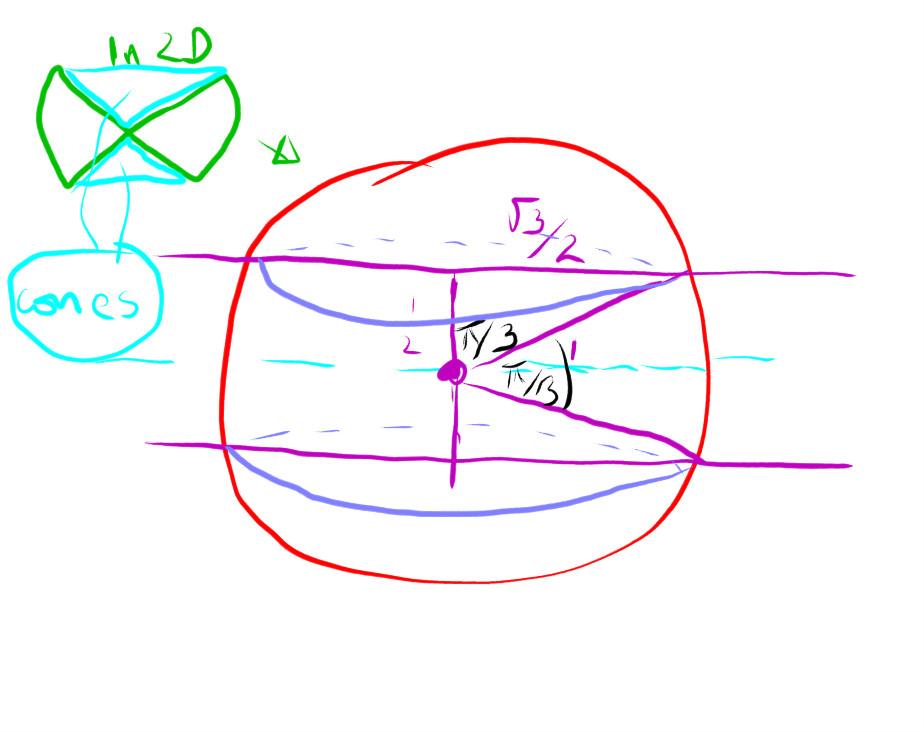
Ive drawn them in in blue as this is rather messy
Using
for each cone
EDITED
So the 2 cones add up to
So new volume
EDITED
Explanation:
Calculating the revolution volume generated by the rotation of


