What is the equation of the tangent line of f(x)= x^2-3x+(3x^3)/(x-7) at x=2?
1 Answer
Jul 8, 2016
The Tangent line equation
Explanation:
Given
let us solve for the point
At
Let us compute for the slope by derivatives
Slope
The equation of the Tangent line by Point-Slope Form
Kindly see the graph of
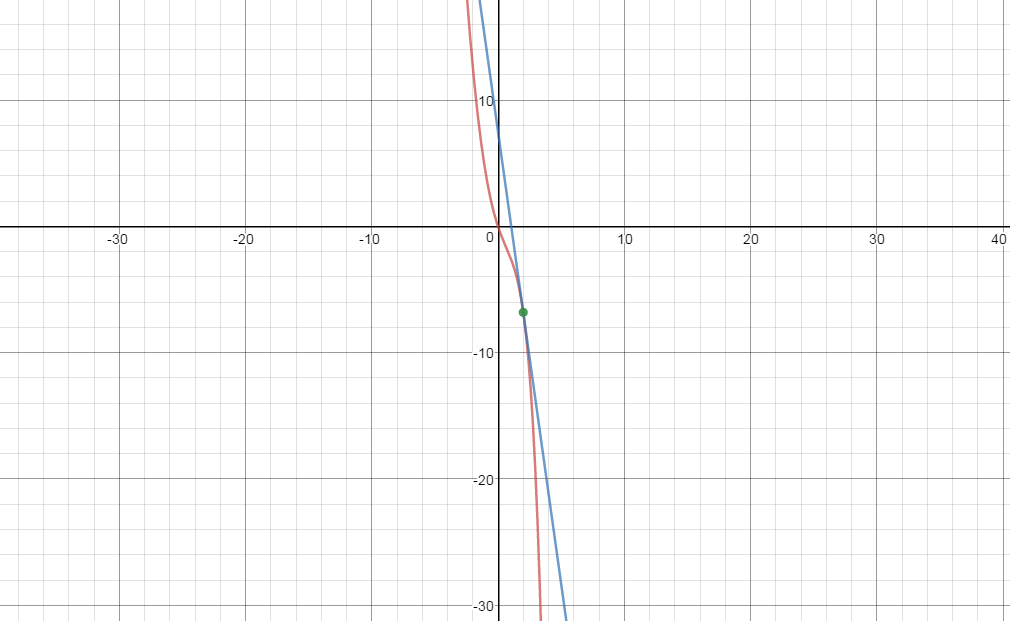 Desmos.com
Desmos.com
God bless....I hope the explanation is useful.
