Question

How do you find the Taylor polynomials of orders 0, 1, 2, and 3 generated by f at a f(x) = cos(x), a= pi/4?

Answer 1

`cos(x) =`

`sqrt(2)/2 - (sqrt(2)/(2)(x-pi/4))/(1!) - (sqrt(2)/(2)(x-pi/4)^(2))/(2!)+ (sqrt(2)/(2)(x-pi/4)^(3))/(3!) + ...`

`=sum_(n=0)^(∞) (f^(n)(pi/4) (x-pi/4)^(n))/(n!)`

Explanation:

Remembering that any function `f(x)` can be expressed as an infinite sum centered at a specific point `a` is found using the formula

`f(x) = f(a) + (f^(1)(a) (x-a)^(1))/(1!)+ (f^(2)(a) (x-a)^(2))/(2!)+ ...`

We can compute the required derivatives (in this case three) and find a general formula for our infinite sum.

Calculations:

`f(x) = cos(x) -> f(pi/4) .......................................= sqrt(2)/(2)`

`f^(1)(x) = -sin(x) -> f^(1)(pi/4) ............................... = - sqrt(2)/(2)`

`f^(2)(x) =-cos(x) -> f^(2)(pi/4) ...............................= - sqrt(2)/(2)`

`f^(3)(x) = sin(x) -> f^(3)(pi/4) .....................................= sqrt(2)/(2)`

Now that we have our derivatives at point `x=pi/4`, we can construct our four terms:

`cos(x) =`

`sqrt(2)/2 - (sqrt(2)/(2)(x-pi/4))/(1!) - (sqrt(2)/(2)(x-pi/4)^(2))/(2!)+ (sqrt(2)/(2)(x-pi/4)^(3))/(3!) + ...`

`=sum_(n=0)^(∞) (f^(n)(pi/4) (x-pi/4)^(n))/(n!)`

To check our answer, we can always graph both equations:

Graph of `cos x`

graph{cos x [-7.9, 7.895, -3.95, 3.95]}

Graph of `sqrt(2)/2 - (sqrt(2)/(2)(x-pi/4))/(1!) - (sqrt(2)/(2)(x-pi/4)^(2))/(2!)+ (sqrt(2)/(2)(x-pi/4)^(3))/(3!)`

graph{sqrt(2)/(2) - (sqrt(2)/(2)(x-pi/4))/(1!) - (sqrt(2)/(2)(x-pi/4)^(2))/(2!)+ (sqrt(2)/(2)(x-pi/4)^(3))/(3!) [-7.9, 7.895, -3.95, 3.95]}

Overlapping both graphs gives you the following:

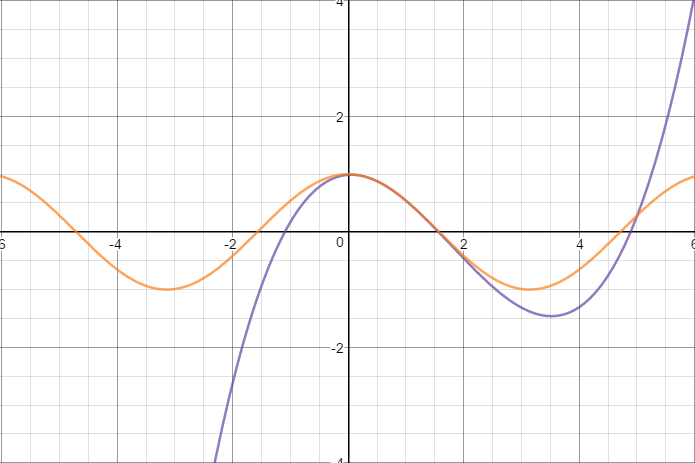
If we increase the number of polynomial terms in our series we automatically make it a better approximation to our function.