How do you evaluate the integral int x/(sqrt(16-x^2)dx from 0 to 4?
3 Answers
Explanation:
For this particular integral, we can use a trigonometric substitution.
If we have the form
If it helps, you can use a triangle to to visualize this:
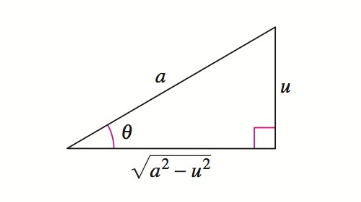
Since we have the integral
Let
Also note that
Therefore, also changing the limits of integration, we can write
Remembering that
By looking at the triangle, we can see that
= -4[sqrt(16-16)/(4) - sqrt(16-0)/(4)]
= -4[0-4/4] = -4[-1] = 4
Explanation:
Although it is a possibility, a trigonometric substitution is not necessary.
This can also be tackled using the substitution
int_0^4x/sqrt(16-x^2)dx=-1/2int_0^4(-2x)/sqrt(16-x^2)dx
Before making the
-1/2int_0^4(-2x)/sqrt(16-x^2)dx=-1/2int_16^0 1/sqrtudu
From here, we can reorder the integral using the rule:
-1/2int_16^0 1/sqrtudu=1/2int_0^16u^(-1/2)du
From here, integrate using the rule:
1/2int_0^16u^(-1/2)du=1/2[u^(-1/2+1)/(-1/2+1)]_0^16=1/2[u^(1/2)/(1/2)]_0^16
The
1/2[u^(1/2)/(1/2)]_0^16=[sqrtu]_0^16=sqrt16-sqrt0=4
as a mere third approach, but one where you can pretty much do the heavy lifting in your head, provided you're up for a bit of pattern recognition....
we have
and from the power rule
IOW!!
so
whilst the other 2 answers have been beautifully presented and are very elegant, my suggestion is this .... well, they didn't say you had to use a trig sub here, or any sub for that matter, and you don't have to so why bother?
and these patterns show up all over the place.



