What is the equation of the normal line of #f(x)=2x^4+4x^3-2x^2-3x+3# at #x=1#?
2 Answers
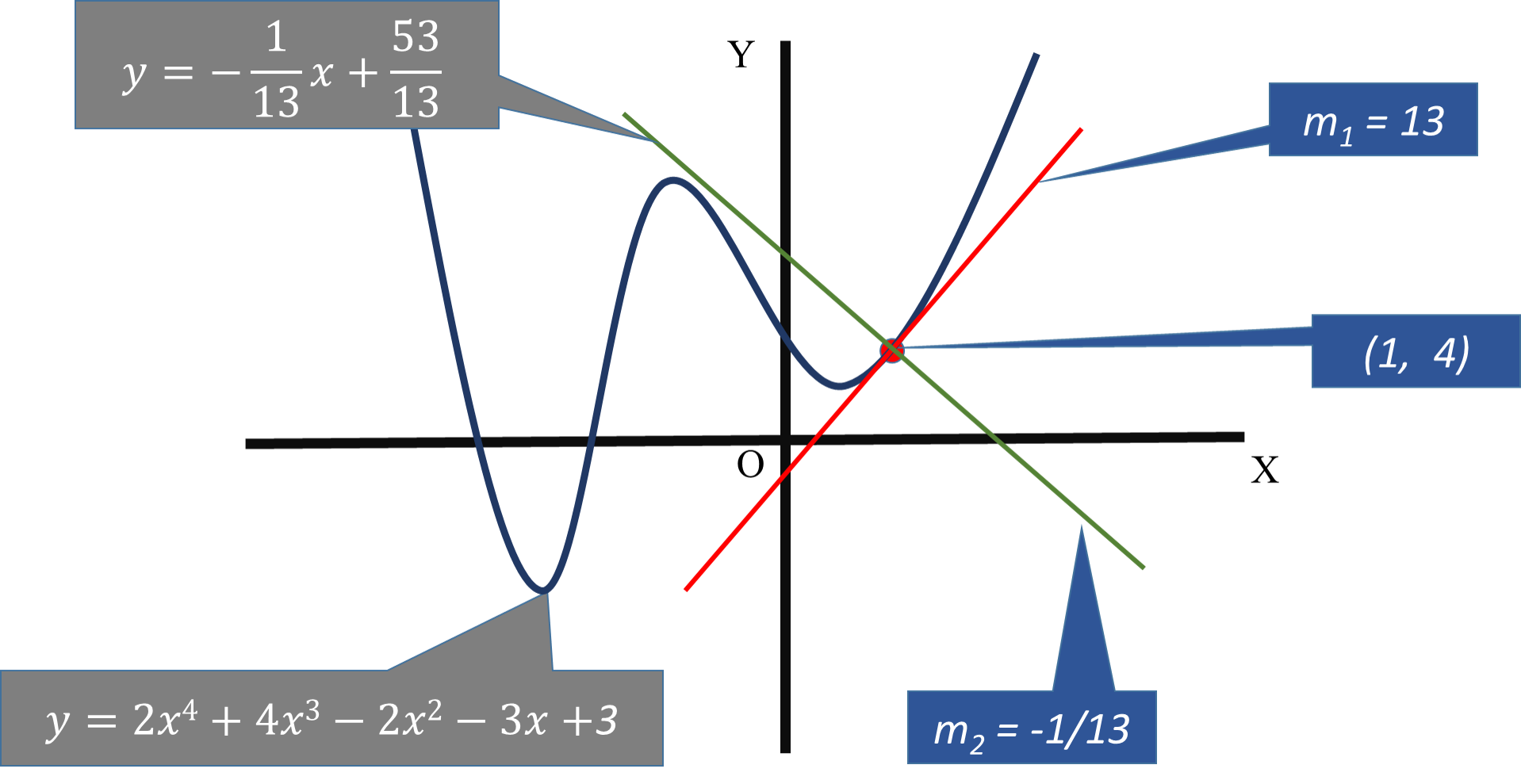
#y=-1/13x+53/13#
Explanation:
Given -
#y=2x^4+4x^3-2x^2-3x+3#
The first derivative gives the slope at any given point
#dy/dx=8x^3+12x^2-4x-3#
At
#m_1=8(1^3)+12(1^2)-4(1)-3#
#m_1=8+12-4-3=13#
This is the slope of the tangent drawn to the point
The y-coordinate at
#y=2(1^4)+4(1^3)-2(1^2)-3(1)+3#
#y=2+4-2-3+3=4#
The normal and the tangent are passing through the point
The normal cuts this tangent vertically. Hence, its slope must be
#m_2=-1/13#
[You must know the product of the slopes of the two vertical lines is
The equation of the normal is -
#-1/13(1) +c=4#
#c=4+1/13=(52+1)/13=53/13#
#y=-1/13x+53/13#
Explanation:
To find the equation to the normal First step is to find the slope.
The first derivative of a curve at a particular point is the slope of the
tangent at that point.
Use this idea let us first find the slope of the tangent
The slope of the tangent to the given curve at x=1 is 13
The product of the slopes of the tangent and normal would be -1 .
so the slope of the normal is
we need to find f(x) at
we have slope is
We have


