Your teacher made 8 triangles he need help to identify what type triangles they are. Help him?: 1) #12, 16, 20# 2) #15, 17, 22# 3) #6, 16, 26# 4) #12, 12, 15# 5) #5,12,13# 6) #7,24,25# 7) #8,15,17# 8) #9,40,41#

Let's say your teacher told you that he made the 8 triangles but he does not know what type triangles they are. Can you help him identify what type of triangles she made:
1) #12, 16, 20#
2) #15, 17, 22#
3) #6, 16, 26#
4) #12, 12, 15#
5) #5,12,13#
6) #7,24,25#
7) #8,15,17#
8) #9,40,41#

2 Answers
P dilip_k
Aug 18, 2016

According to Pythagoras theorem we have the following relation for a right angled triangle.

#"hypotenuse"^2= "sum of square of other smaller sides"#

This relation holds good for
triangles #1,5,6,7,8->"Right angled"#
They are also Scalene Triangle as their three sides are unequal in length.

#(1)->12^2+16^2=144+256=400=20^2#

#(5)->5^2+12^2=25+144=169=13^2#

#(6)->7^2+24^2=49+576=625=25^2#

#(7)->8^2+15^2=64+225=289=17^2#

#(8)->9^2+40^2=81+1600=1681=41^2#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#(3)->6+16<26->"Triangle not possible"#

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

#(2)->15!=17!=22->"Scalene triangle"#

#(4)->12=12!=15->"Isosceles triangle"#

A08
Aug 18, 2016

1) #12,16,20#: Scalene, right triangle
2) #15,17,22#: Scalene
3) #6,16,26#: Triangle does not exist.
4) #12,12,15#: Isosceles
5) #5,12,13#: Scalene, right triangle
6) #7,24,25#: Scalene, right triangle
7) #8,15,17#: Scalene, right triangle
8) #9,40,41#: Scalene, right triangle

Explanation:

From a theorem we know that
The sum of the lengths of any two sides of a triangle must be greater than the third side. If this is not true, triangle does not exist.
We test the given set of values in each instance and notice that in case of
3) #6,16,26# the condition is not met as
#6+16 # is not# > 26#.

To identify different types of triangles either by way of given lengths of its sides or measure of its three angles is shown below:
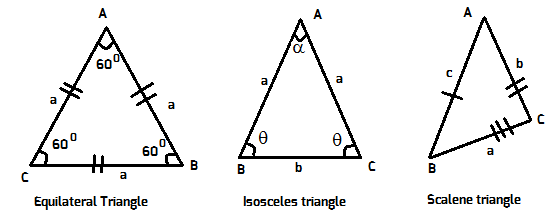
2.bp.blogspot.com

In the problem three sides of each triangle are given. As such we will identify these by sides.

1) #12,16,20#: All three sides are of unequal lengths, therefore Scalene
2) #15,17,22#: All three sides are of unequal lengths, therefore Scalene
3) #6,16,26#: Triangle does not exist.
4) #12,12,15#: Two sides are of equal lengths, therefore Isosceles
5) #5,12,13#: All three sides are of unequal lengths, therefore Scalene
6) #7,24,25#: All three sides are of unequal lengths, therefore Scalene
7) #8,15,17#: All three sides are of unequal lengths, therefore Scalene
8) #9,40,41#: All three sides are of unequal lengths, therefore Scalene

There is a fourth category of triangles in which one of interior angles is of #90^@#.
It is called right triangle.
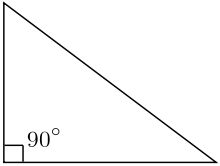
wikipedia
It can be either be Scalene or Isosceles.

We know from Pythagoras theorem that for a right triangle

Square of largest side#=#Sum of squares of other two sides

Now testing sides of each triangle
1) #12,16,20#: #20^2=16^2+12^2#: True, hence right triangle.
2) #15,17,22#: #22^2!=15^2+17^2#: hence not right triangle.
4) #12,12,15#: #15^2!=12^2+12^2#: hence not right triangle.
5) #5,12,13#: #13^2=5^2+12^2#: True, hence right triangle.
6) #7,24,25#: #25^2=7^2+24^2#: True, hence right triangle.
7) #8,15,17#: #17^2=8^2+15^2#: True, hence right triangle.
8) #9,40,41#: #41^2=9^2+40^2#: True, hence right triangle.

Combining three steps we state the answer.

Related questions
See all questions in Solving Modeling Problems with Similar and Congruent Triangles
Impact of this question
8282 views around the world
You can reuse this answer
Creative Commons License