How do you divide #(x^4-11x^3-49x^2+899x-2506)-:(x-8)#?
1 Answer
#(x^4-11x^3-49x^2+899x-2506) -: (x-8)#
#= (x^3-3x^2-73x+315)+14/(x-8)#
Explanation:
You can write out the quotient term by term, adding up the partial sums as you go along. This is a form of synthetic division doing the work in your head...
#x^4-11x^3-49x^2+899x-2506#
#=(x-8)(x^3... " "# to match the leading#x^4# term
#=(x-8)(x^3-3x^2... " "# to match the#x^3# term
#=(x-8)(x^3-3x^2-73x... " "# to match the#x^2# term
#=(x-8)(x^3-3x^2-73x+315)... " "# to match the#x# term
#=(x-8)(x^3-3x^2-73x+315)+14 " "# to match the constant term
OK, some of the "in your head" arithmetic was a little challenging, e.g.
We can also do this by long dividing the coefficients...
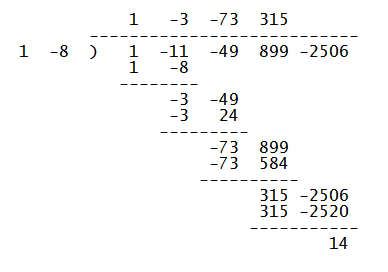
This way you get to write down your workings as you go along.
In any case, we find:
#x^4-11x^3-49x^2+899x-2506=(x-8)(x^3-3x^2-73x+315)+14#
So:
#(x^4-11x^3-49x^2+899x-2506) -: (x-8)#
#= (x^3-3x^2-73x+315)+14/(x-8)#

