Call #S = sum_1^oo y^(n)/(1+n^(2))# then
#sum_1^oo abs(y^n)/(1+n^(2)) < sum_1^oo abs(y^n)/n^2# so
if #sum_1^oo abs(y^n)/n^2# converges then #sum_1^oo abs(y^n)/(1+n^(2))# also converges.
Calling #S_1 = sum_1^oo y^n/n^2# we have
#y(d/(dy)S_1)=sum_1^oo y^n/n# and
#y d/(dy)(y(d/(dy)S_1)) = sum_1^oo y^n#
supposing now that #abs(y) < 1# we have
#y d/(dy)(y(d/(dy)S_1)) =1/(1-y)-1 = y/(1-y)#
and successively
#d/(dy)(y(d/(dy)S_1)) =1/(1-y)#
#y(d/(dy)S_1) =-log_e(1-y)#
#d/(dy)S_1 =-log_e(1-y)/y#
#S_1 = "PolyLog"(2,y)#
So for #abs (3x-2) < 1# this series is convergent with convergence radius
#1/3 < x < 1#
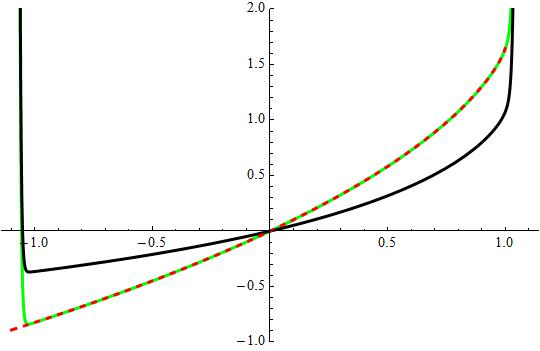
Attached a plot showing #S# in black and #S_1, "PolyLog(2,y)"# in green and dashed red respectively.