What are all the possible rational zeros for #f(x)=x^5+2x^4+14x^3+26x^2+40x+80# and how do you find all zeros?
1 Answer
Find there are no rational zeros. Can use a numerical method to find approximations.
Explanation:
By the rational roots theorem, any rational zeros of
In addition note that all of the coefficients of
So the only possible rational zeros of
#-1, -2, -4, -5, -8, -10, -16, -20, -40, -80#
None of these work, so
Typically for a quintic or polynomial of higher degree, the zeros of
About the best you can do is find numerical approximations using a method such as Durand-Kerner to find:
#x_1 ~~ -1.92974#
#x_(2,3) ~~ -0.135287+-3.0955i#
#x_(4,5) ~~ 0.100156+-2.07561i#
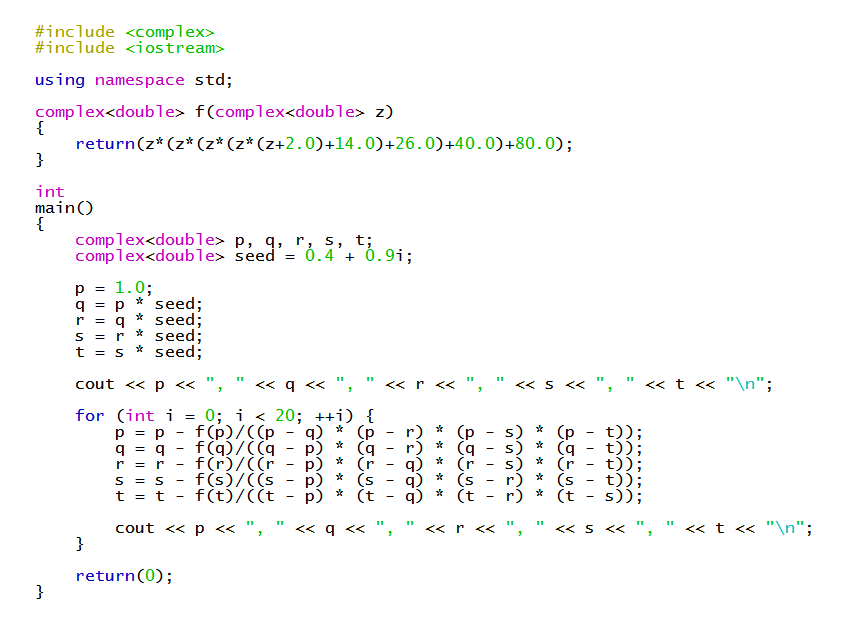
For more details on using Durand-Kerner to find such zeros of a quintic, see https://socratic.org/s/axney67c
Here's an example C++ program that implements the Durand-Kerner algorithm for our current example...