Question

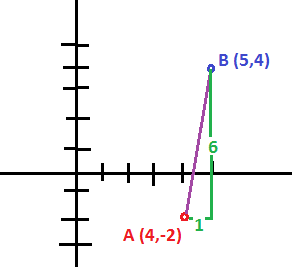
Objects A and B are at the origin. If object A moves to `(4 ,-2 )` and object B moves to `(5 ,4 )` over `8 s`, what is the relative velocity of object B from the perspective of object A? Assume that all units are denominated in meters.

Answer 1

Velocity: `0.7603` m/sec at `80.54^@` (measuring counter clockwise from the X-axis)

Explanation:

Note that it doesn't matter that `A` and `B` started at the origin; it only matters that they started at the same place.

The initial distance between `A` and `B` is `0` (meters)
The distance between `A` and `B` after `8` seconds is
`color(white)("XXX")sqrt((5-4)^2+(4-(-2))^2)=sqrt(37)` (meters)

Since this is the change in position relative to each other
the relative speed of `B` from `A`'s perspective is
`color(white)("XXX")(sqrt(37) "meters")/(8 "seconds") ~~0.7603453 "m/sec"`

The tan of the angle (relative to the horizontal/X-axis) is `6/1` (see diagram below).

Therefore the angular component of the velocity is
`color(white)("XXX")"arctan"(6) ~~80.53768^@`