An object with a mass of #4 kg# is acted on by two forces. The first is #F_1= < -4 N , 5 N># and the second is #F_2 = < 1 N, -8 N>#. What is the object's rate and direction of acceleration?

Question

1155 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-09-27T08:35:11

#vec a=(3 sqrt(2))/4 " "m/s^2#

#alpha=180+45=225 ^o " with positive x direction"#

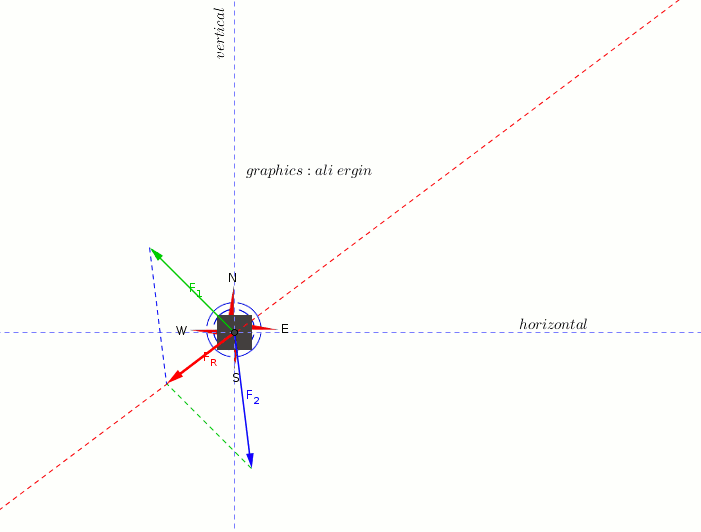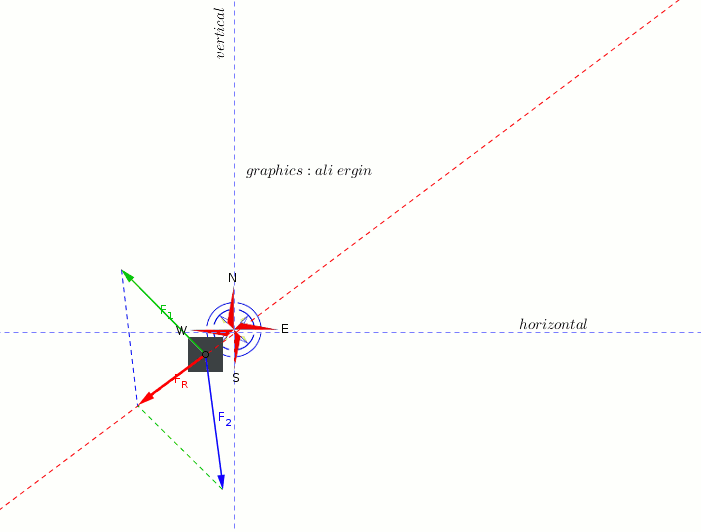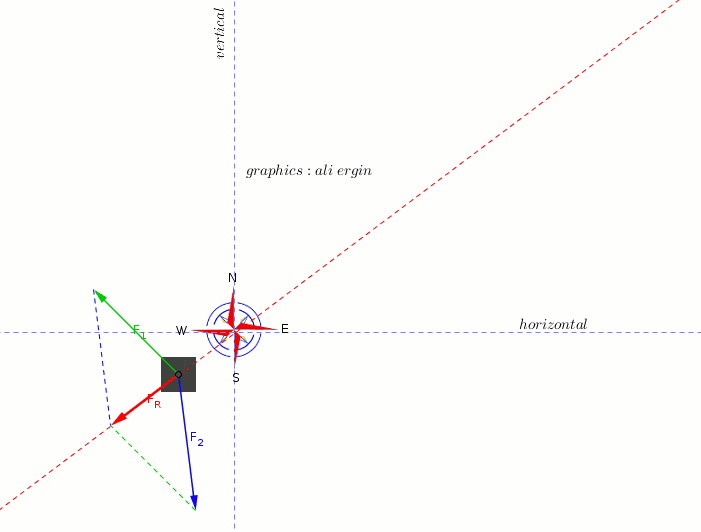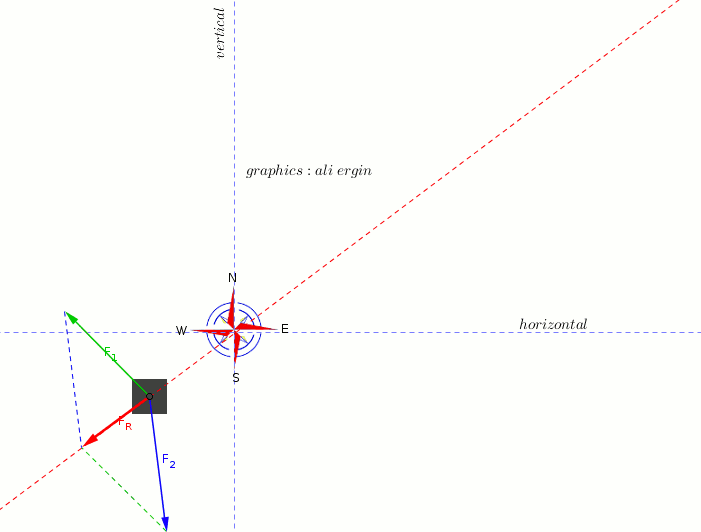
enter image source here

#F_1=<-4N,5N>#
#F_(1x)=-4N#
#F_(1y)=5N#

#F_2=<1N,-8N>#
#F_(2x)=1N#
#F_(2y)=-8N#

#"The vectorial sum of the horizontal components :"#

#Sigma vec F_x=vec F_(1x)+vec F_(2x)#

#Sigma vec F_x=-4+1=-3N#

#"The vectorial sum of the vertical components :"#

#Sigma vec F_y=vec F_(1y)+vec F_(2y)#

#Sigma vec F_y=5-8=-3N#

#"The magnitude of the resultant Force :"#

#F_R=sqrt(Sigma vec F_x+Sigma vec F_y)#

#F_R=sqrt((-3)^2+(-3)^2)#

#F_R=sqrt(9+9)#

#F_R=3sqrt2" N"#

#"You can use the Newton's second law to calculate acceleration"#

#vec a:"acceleration"#
#m:"mass"#
#vec F_R:"Force"#

#vec a=vec F_R/m#

#vec a=(3 sqrt(2))/4 " "m/s^2#

#"Direction :"#

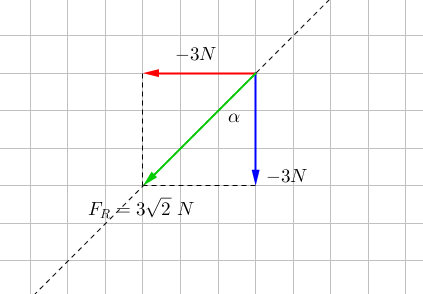
enter image source here

#tan alpha=(-3)/(-3)=1#

#alpha=180+45=225 ^o " with positive x direction"#