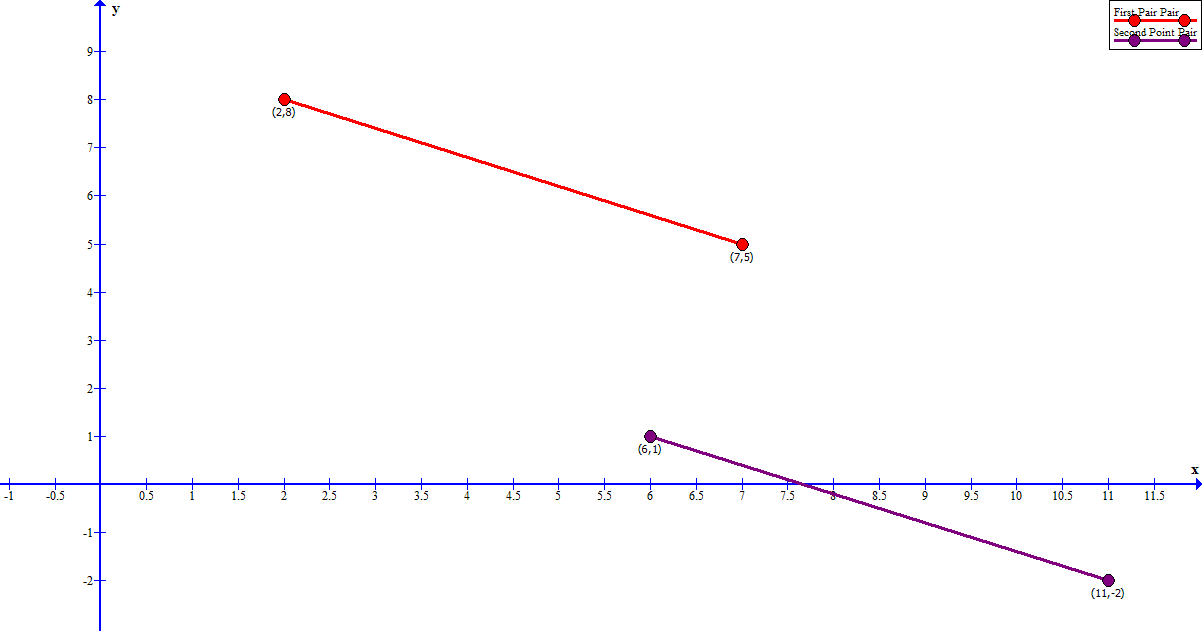
A line passes through #(2 ,8 )# and #( 7, 5 )#. A second line passes through #( 6, 1 )#. What is one other point that the second line may pass through if it is parallel to the first line?

2 Answers
Lil Del
Oct 5, 2016

#(11, -2)# is a point through which the second line might pass.

Explanation:

Parallel lines have equal slopes, so the first step is to find the slope of the line which passes through (#2, 8)# and #(7, 5)# using the slope formula. The formula for slope, #m#, is:
#m = (y_2 - y_1)/(x_2 - x_1)#

Substitute the known coordinates:
#m = (5 -8)/(7 - 2)#
#m = (-3)/5#

Remember that slope is "rise over run", so the numerator of the slope can be added to the #y#-coordinate of the known point and the denominator of the slope can be added to the #x#-coordinate of the known point to find another point on the other line.

#(6 + 5, 1 + -3)#
#(11, -2)#

So, #(11, -2)# is a point through which the second line might pass.

Alan P.
Oct 5, 2016

#color(green)(""(11,-2))#

Explanation:

Slope of line through #(2,8)# and #(7,5)#
#color(white)("XXX")m=(Deltay)/(Deltax)= (8-5)/(2-7)=-3/5#

This means that a change #Deltax=5# would correspond to a change #Deltay=-3#

So #(6+Deltax,1+Deltay)# would be a point #(11,-2)#

enter image source here

Related questions
See all questions in Equations of Parallel and Perpendicular Lines
Impact of this question
1892 views around the world
You can reuse this answer
Creative Commons License