How do you find the equation of the parabola having its focus at #( 1/2, 1/2)# and the directrix along #x - y = 1#?
2 Answers
Explanation:
Calling the directrix as
and the symmetry line
we have
Solving for
Now, the parabola is the place where the distance between a generic plane point
but
where
giving
Attached the parabola plot
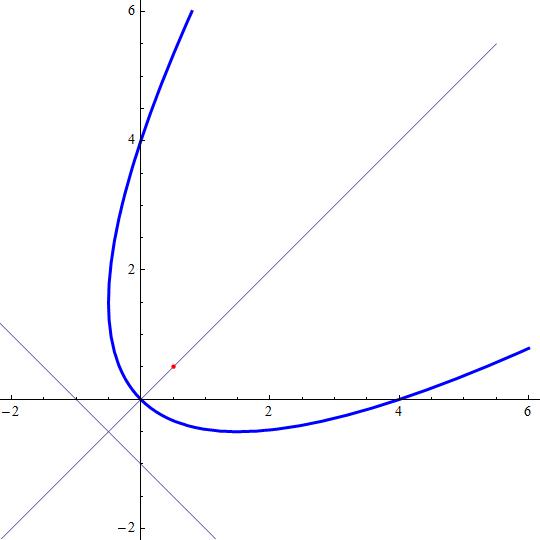
Explanation:
Let (x, y) be a point on the parabola.
Using that its distance from the focus equals the distance from the
directrix,
parabola. Squaring,
The vertex V of the parabola is on the perpendicular SX from the
focus S(1/2, 1/2), on the directrix DX given by x-y=1. The equation of
the perpendicular is of the form x+y=c. As S(1/2, 1/2) lies on this, c = 1.
V bisects SX.
So, V is (3/4, 1/4).. The size of the parabola
a = VS =

