Given #f(x) = x^3-3x#, how can you construct an infinitely differentiable one-one function #g(x):RR->RR# with #g(x) = f(x)# in #(-oo, -2] uu [2, oo)#?
4 Answers
Here is my first attempt. (Unfortunately, it fails.)
Explanation:
graph{x^3-3x [-5.454, 5.645, -2.606, 2.94]}
My first thought is for a piecewise function, keeping the definition of
I tried a piece based on
We need
and
Determined to find a polynomial, I set
#g(x)=ax^n# where#n# is odd
So,
We need
This lead to
But for infinite differentiability, we also need
#g''(2) =-12# and# g''(2) = 12#
#g'''(-2) = g'''(2) = 6#
#g^((n))(-2) = g^((n))(2) = 0# for#n>= 4# .
This attempt fails to satisfy those.
My initial thought was to try something using
Perhaps we can start with and odd, four-times integrable function and work backwards from there.
So
Explanation:
This makes
(All integrals by Wolfram Alpha) And
(Note:
#g''(+-2) = 3/4(+-2)(8) = +-12# )
Never mind.
What was I thinking?
See below.
Explanation:
For practical purposes and with a guarantee of accuracy, we can proceed, according to
This for
Solving this system we obtain
So the binding function is
Attached a plot showing the binding.
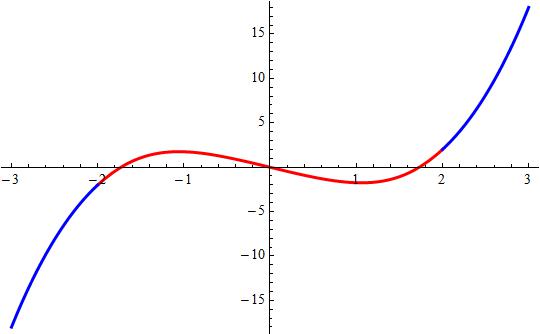
Explanation:
A classic example of a function for which the Taylor series fails is:
#j(x) = { (0, " if " x = 0), (e^(-1/x^2), " if " x != 0) :}#
This has the property that the function and all of its derivatives exist and are
Inspired by this, consider the function:
#h(x) = { (0, " if " x = +-2), (e^(-x^2/(x^2-4)^2), " otherwise") :}#
Then
graph{e^(-x^2/(x^2-4)^2) [-5, 5, -2.5, 2.5]}
Given
Define
#g(x) = { (f(x), " if " x in (-oo, -2] uu [2, oo)), (f(x)+h(x)(x^9/256-f(x))(1+x^2/(x^2-4)^2+x^4/(2(x^2-4)^4)), " if " x in (-2, 2)) :}#
The idea here is that
graph{x^3-3x+e^(-x^2/(x^2-4)^2)*(x^9/256+3x-x^3)(1+x^2/(x^2-4)^2+x^4/(2(x^2-4)^4)) [-5, 5, -2.5, 2.5]}
The additional trick here is that the multiplier:
#(1+x^2/(x^2-4)^2+x^4/(2(x^2-4)^4))#
is a sufficiently good approximation to
As a result, we do not lose the smoothing properties of
It remains to show that the resulting function is monotonically increasing.



