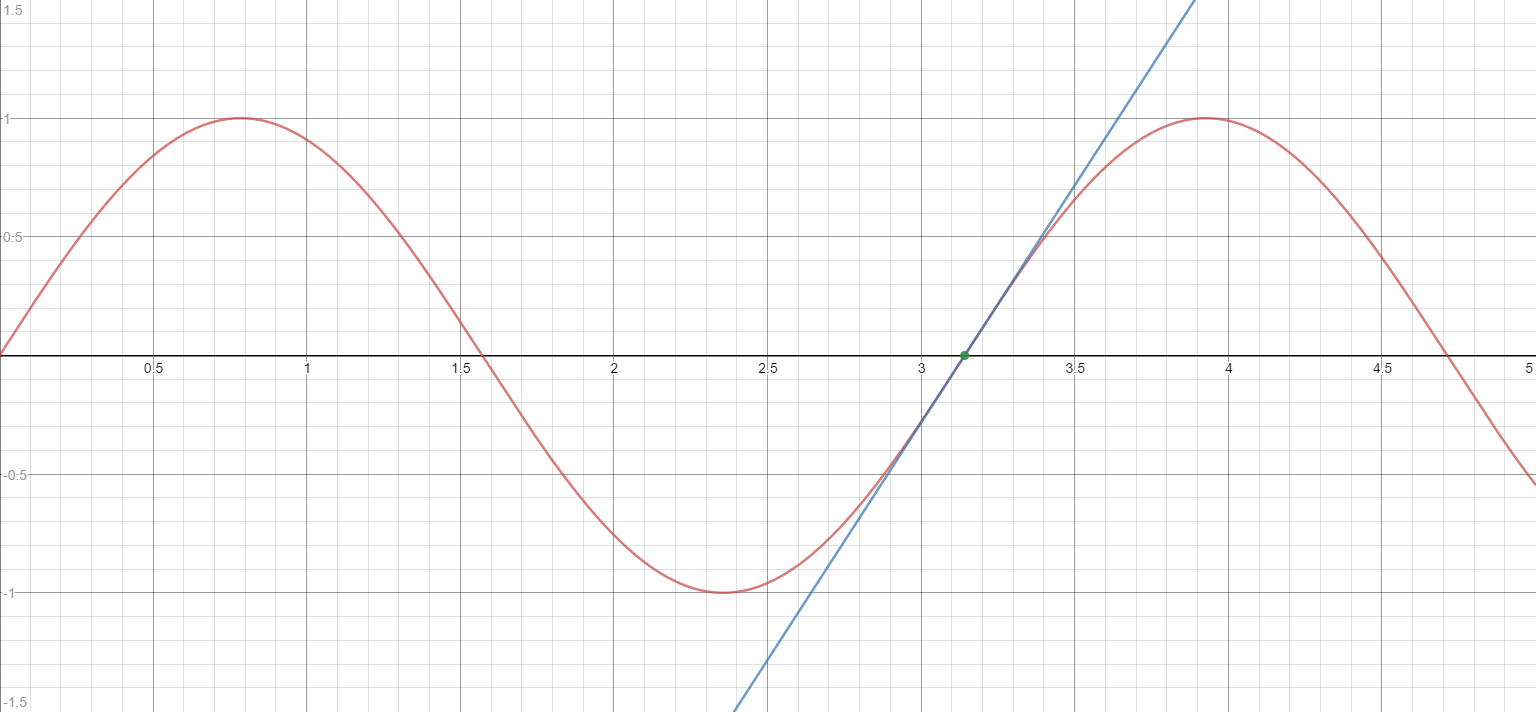
How do you find the equation of the tangent line of the function #f(x) = sin(2x)# when given the point (#pi,0#)?

How do you find the equation of the tangent line of the function #f(x) = sin(2x)# when given the point (#pi,0#)?

1 Answer
sente
Oct 12, 2016

#y = 2x-2pi#

Explanation:

The tangent line of a curve #y=f(x)# at a point #(x_1, f(x_1))# has a slope of #f'(x_0)#. Using that, together with the point-slope form of the equation of a line #y-y_1 = m(x-x_1)#, we can solve for the equation of the tangent line at the given point as

#y = f'(x_1)x-x_1f'(x_1)+f(x_1)#

As we are given #(x_1, f(x_1)) = (pi, 0)#, all that remains is to find #f'(pi)#.

Using that #d/dxsin(x) = cos(x)# along with #d/dx cx = c# and the chain rule, we find

#f'(x) = d/dxsin(2x)#

#=cos(2x)(d/dx2x)#

#=2cos(2x)#

Thus #f'(pi) = 2cos(2pi) = 2#

Plugging this into our equation for the tangent line, we get

#y = 2x-pi(2)+0#

#=> y = 2x-2pi#

Graphed together:

enter image source here

Related questions
See all questions in Tangent Line to a Curve
Impact of this question
4363 views around the world
You can reuse this answer
Creative Commons License